《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

1. 下列运算正确的是 (B)
A.$ 3x^{2}\cdot 2x^{3}= 5x^{6} $
B.$ (3x^{3})^{2}= 9x^{6} $
C.$ 3^{-2}= \frac{1}{6} $
D.$ 5^{0}= 0 $

答案： A. $3x^{2} \cdot 2x^{3} = 6x^{5}$，错误；
B. $(3x^{3})^{2} = 9x^{6}$，正确；
C. $3^{-2} = \frac{1}{9}$，错误；
D. $5^{0} = 1$，错误。
答案：B

2. 对于下列说法,正确的是 (B)
A.在同一平面内,过一点有且只有一条直线与已知直线平行
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.测量孙浩的跳远成绩,正确做法的依据是基本事实“两点之间,线段最短”
D.不相交的两条直线叫做平行线

答案： A. 在同一平面内，过直线外一点有且只有一条直线与已知直线平行，原说法错误。
B. 在同一平面内，过一点有且只有一条直线与已知直线垂直，说法正确。
C. 测量跳远成绩依据的是“垂线段最短”，原说法错误。
D. 在同一平面内，不相交的两条直线叫做平行线，原说法错误。
答案：B

3. 如图,在数轴上有A,B,C,D四个整数点(即各点均表示整数),且$ 2AB= BC= 3CD $,若A,D两点表示的数分别为-5和6,那么该数轴上点C表示的整数是 (B)

A.-2
B.4
C.-4
D.2

答案： 解：设 $ CD = x $，则 $ BC = 3CD = 3x $，$ 2AB = BC $，所以 $ AB = \frac{3x}{2} $。
因为 $ A $，$ D $ 两点表示的数分别为 -5 和 6，所以 $ AD = 6 - (-5) = 11 $。
又因为 $ AD = AB + BC + CD $，即 $ \frac{3x}{2} + 3x + x = 11 $，解得 $ x = 2 $。
所以 $ CD = 2 $，因为 $ D $ 表示的数为 6，所以点 $ C $ 表示的数为 $ 6 - 2 = 4 $。
答案：B

4. 如图,$ AB// CD $,$ ∠AFE= 135^{\circ} $,$ ∠D= 80^{\circ} $,则$ ∠E $等于 (A)
A.$ 55^{\circ} $
B.$ 45^{\circ} $
C.$ 80^{\circ} $
D.$ 50^{\circ} $

答案： 解：
∵AB//CD，∠AFE=135°
∴∠CGF=∠AFE=135°（两直线平行，同位角相等）
∵∠CGF是△EGD的外角
∴∠CGF=∠E+∠D
∵∠D=80°
∴∠E=∠CGF-∠D=135°-80°=55°
答案：A

5. 关于x,y的方程组$ \begin{cases}2x+y= 4,\\x+2y= -3m+2\end{cases} 的解满足 x-y＞-\frac{3}{2} $,则m的最小整数解为 (C)
A.-3
B.-2
C.-1
D.0

答案： 解：$\begin{cases}2x + y = 4 &①\\x + 2y = -3m + 2 &②\end{cases}$
① - ②，得$x - y = 3m + 2$
因为$x - y ＞ -\frac{3}{2}$，所以$3m + 2 ＞ -\frac{3}{2}$
$3m ＞ -\frac{3}{2} - 2$
$3m ＞ -\frac{7}{2}$
$m ＞ -\frac{7}{6}$
则m的最小整数解为-1
C

6. 在数学中,为了书写简便,18世纪数学家欧拉就引进了求和符合“$ \sum $”,如记$ \sum_{k= 1}^{n}k= 1+2+3+…+(n-1)+n $;$ \sum_{k= 3}^{n}(x+k)= (x+3)+(x+4)+…+(x+n) $.已知$ \sum_{k= 2}^{n}[(x+k)(x-k+1)]= 4x^{2}+4x+m $,则m的值是 (C)
A.40
B.-70
C.-40
D.-20

答案： 解：$\sum_{k=2}^{n}[(x+k)(x - k + 1)]$
$=(x+2)(x-1)+(x+3)(x-2)+(x+4)(x-3)+(x+5)(x-4)$
$=(x^2 + x - 2)+(x^2 + x - 6)+(x^2 + x - 12)+(x^2 + x - 20)$
$=4x^2 + 4x - 40$
对比$4x^2 + 4x + m$，得$m = -40$
答案：C

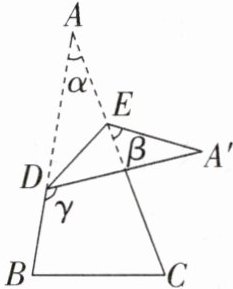
7. 如图,将一张三角形纸片ABC的一角折叠,使点A落在$ △ABC $外的 A' 处,折痕为DE.如果$ ∠A= α $,$ ∠CEA'= β $,$ ∠BDA'= γ $,那么下列式子中正确的是 (A)

A.$ γ=2α+β $
B.$ γ=α+2β $
C.$ γ=α+β $
D.$ γ=180^{\circ}-α-β $

答案： 解：由折叠性质得∠A=∠A'=α。
在△A'ED中，∠AED=∠A'ED。
设∠AED=∠A'ED=x，则∠DEC=180°-x。
在△CEA'中，∠A'EC=β，∠A'ED=∠DEC+∠A'EC，即x=(180°-x)+β，解得x=(180°+β)/2。
∠ADE=180°-∠A-∠AED=180°-α-(180°+β)/2=90°-α-β/2。
∠BDA'=180°-2∠ADE=180°-2×(90°-α-β/2)=2α+β。
结论：γ=2α+β，选A。

8. 大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如$ 2^{3}= 3+5 $,$ 3^{3}= 7+9+11 $,$ 4^{3}= 13+15+17+19 $,…,若$ m^{3} $分裂后,其中有一个奇数是103,则m的值是 (B)
A.9
B.10
C.11
D.12

答案： 观察规律：$2^3$分裂为2个连续奇数，$3^3$分裂为3个连续奇数，$m^3$分裂为m个连续奇数。
$2^3$起始奇数：3=2×1+1；$3^3$起始奇数：7=3×2+1；$4^3$起始奇数：13=4×3+1；...
归纳得$m^3$起始奇数为$m(m-1)+1$，结束奇数为$m(m-1)+1+2(m-1)=m(m+1)-1$。
当$m=10$时，起始奇数$10×9+1=91$，结束奇数$10×11-1=109$，103在91~109之间。
答案：B

9. 一个锐角为$ 55^{\circ} $,这个锐角的补角是125°.

答案： 解：因为互为补角的两个角之和为$180^{\circ}$，已知一个锐角为$55^{\circ}$，所以这个锐角的补角是$180^{\circ} - 55^{\circ} = 125^{\circ}$。
125°

10. 已知$ 3^{a}= 6 $,$ 3^{b}= 2 $,则$ 3^{2a-b} $的值为18.

答案： 解：因为$3^{a}=6$，所以$3^{2a}=(3^{a})^{2}=6^{2}=36$。
又因为$3^{b}=2$，所以$3^{2a - b}=3^{2a}÷3^{b}=36÷2=18$。
18

11. 下面有三个命题:①同旁内角互补,两直线平行;②二元一次方程组的解是唯一的;③平方后等于9的数一定是3.其中①是真命题(填序号).

答案： ①