第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
19. (8分)某商场元旦搞促销活动,活动方案如下表:
|一次性购物|优惠方案|
|不超过200元|不给优惠|
|超过200元,而不超过500元|超过200元的部分按9折优惠|
|超过500元,而不超过1000元|其中500元按9折优惠,超过部分按8折优惠|
|超过1000元|其中1000元按8.5折优惠,超过部分按7折优惠|
(1)此人第一次购买了价值450元的物品,请问应付多少钱?
(2)此人第二次购物付了920元,则购买了价值多少钱的物品?
(3)若此人一次性购买上述两份物品,是更节省还是亏损?节省或亏损多少元?
|一次性购物|优惠方案|
|不超过200元|不给优惠|
|超过200元,而不超过500元|超过200元的部分按9折优惠|
|超过500元,而不超过1000元|其中500元按9折优惠,超过部分按8折优惠|
|超过1000元|其中1000元按8.5折优惠,超过部分按7折优惠|
(1)此人第一次购买了价值450元的物品,请问应付多少钱?
(2)此人第二次购物付了920元,则购买了价值多少钱的物品?
(3)若此人一次性购买上述两份物品,是更节省还是亏损?节省或亏损多少元?
答案:
(1) $200 + (450 - 200)×0.9 = 425$(元)
答:第一次购物应付425元。
(2) 设购买物品原价为$x$元。
① 若$500 < x < 1000$,则$500×0.9 + (x - 500)×0.8 = 920$,解得$x = 1087.5$(与假设不符,舍去)。
② 若$x > 1000$,则$1000×0.85 + (x - 1000)×0.7 = 920$,解得$x = 1100$。
答:第二次购物原价为1100元。
(3) 两次物品原价总和:$450 + 1100 = 1550$(元)
合并购买应付:$1000×0.85 + (1550 - 1000)×0.7 = 1235$(元)
分开购买实付:$425 + 920 = 1345$(元)
节省金额:$1345 - 1235 = 110$(元)
答:两次购物合起来买更节省,节省110元。
(1) $200 + (450 - 200)×0.9 = 425$(元)
答:第一次购物应付425元。
(2) 设购买物品原价为$x$元。
① 若$500 < x < 1000$,则$500×0.9 + (x - 500)×0.8 = 920$,解得$x = 1087.5$(与假设不符,舍去)。
② 若$x > 1000$,则$1000×0.85 + (x - 1000)×0.7 = 920$,解得$x = 1100$。
答:第二次购物原价为1100元。
(3) 两次物品原价总和:$450 + 1100 = 1550$(元)
合并购买应付:$1000×0.85 + (1550 - 1000)×0.7 = 1235$(元)
分开购买实付:$425 + 920 = 1345$(元)
节省金额:$1345 - 1235 = 110$(元)
答:两次购物合起来买更节省,节省110元。
20. (12分)如图,已知数轴上有$A$,$B$,$C$三点,分别表示有理数$- 26$,$- 10$,10,动点$P从A$出发,以每秒1个单位的速度向终点$C$移动,设点$P移动时间为t$秒.
(1)用含$t的代数式表示点P$对应的数:
用含$t的代数式表示点P和点C$之间的距离:$PC = $
(2)当点$P运动到B$点时,点$Q从A$点出发,以每秒3个单位的速度向$C$点运动,$Q点到达C$点后,再立即以同样的速度返回点$A$,探究点$P$,$Q$同时运动的过程中是否相遇,若相遇,求相遇时$t$的值.
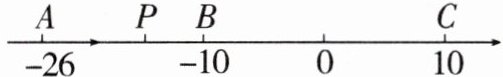
(1)用含$t的代数式表示点P$对应的数:
$-26 + t$
;用含$t的代数式表示点P和点C$之间的距离:$PC = $
$36 - t$
.(2)当点$P运动到B$点时,点$Q从A$点出发,以每秒3个单位的速度向$C$点运动,$Q点到达C$点后,再立即以同样的速度返回点$A$,探究点$P$,$Q$同时运动的过程中是否相遇,若相遇,求相遇时$t$的值.
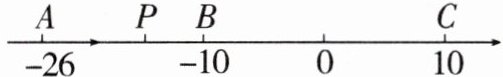
点$P$从$A$到$B$所需时间:$(-10) - (-26) = 16$秒,即$t=16$时$Q$开始运动。
① $Q$返回前相遇($16 \leq t \leq 16 + \frac{10 - (-26)}{3}=28$):
$P$位置:$-10 + (t - 16)$,$Q$位置:$-26 + 3(t - 16)$
相遇时:$-10 + t - 16 = -26 + 3(t - 16)$
解得:$t = 24$
② $Q$返回后相遇($t > 28$):
$Q$返回后位置:$10 - 3(t - 28)$,$P$位置:$-10 + (t - 16)$
相遇时:$-10 + t - 16 = 10 - 3(t - 28)$
解得:$t = 30$
综上,相遇时$t$的值为$24$或$30$。
① $Q$返回前相遇($16 \leq t \leq 16 + \frac{10 - (-26)}{3}=28$):
$P$位置:$-10 + (t - 16)$,$Q$位置:$-26 + 3(t - 16)$
相遇时:$-10 + t - 16 = -26 + 3(t - 16)$
解得:$t = 24$
② $Q$返回后相遇($t > 28$):
$Q$返回后位置:$10 - 3(t - 28)$,$P$位置:$-10 + (t - 16)$
相遇时:$-10 + t - 16 = 10 - 3(t - 28)$
解得:$t = 30$
综上,相遇时$t$的值为$24$或$30$。
答案:
(1) $-26 + t$;$36 - t$
(2) 点$P$从$A$到$B$所需时间:$(-10) - (-26) = 16$秒,即$t=16$时$Q$开始运动。
① $Q$返回前相遇($16 \leq t \leq 16 + \frac{10 - (-26)}{3}=28$):
$P$位置:$-10 + (t - 16)$,$Q$位置:$-26 + 3(t - 16)$
相遇时:$-10 + t - 16 = -26 + 3(t - 16)$
解得:$t = 24$
② $Q$返回后相遇($t > 28$):
$Q$返回后位置:$10 - 3(t - 28)$,$P$位置:$-10 + (t - 16)$
相遇时:$-10 + t - 16 = 10 - 3(t - 28)$
解得:$t = 30$
综上,相遇时$t$的值为$24$或$30$。
(1) $-26 + t$;$36 - t$
(2) 点$P$从$A$到$B$所需时间:$(-10) - (-26) = 16$秒,即$t=16$时$Q$开始运动。
① $Q$返回前相遇($16 \leq t \leq 16 + \frac{10 - (-26)}{3}=28$):
$P$位置:$-10 + (t - 16)$,$Q$位置:$-26 + 3(t - 16)$
相遇时:$-10 + t - 16 = -26 + 3(t - 16)$
解得:$t = 24$
② $Q$返回后相遇($t > 28$):
$Q$返回后位置:$10 - 3(t - 28)$,$P$位置:$-10 + (t - 16)$
相遇时:$-10 + t - 16 = 10 - 3(t - 28)$
解得:$t = 30$
综上,相遇时$t$的值为$24$或$30$。
查看更多完整答案,请扫码查看


