《2025年通城学典课时作业本七年级数学上册苏科版江苏专版》

6. (新情境·游戏活动)如图所示为由同样大小的围棋棋子按照一定规律摆成的“山”字,其中,第1个“山”字需要7枚棋子,第2个“山”字需要12枚棋子,第3个“山”字需要17枚棋子,…,按照此规律,52枚棋子可以摆成 ()

A. 第8个“山”
B. 第9个“山”
C. 第10个“山”
D. 第11个“山”

答案： A 解析：第n个“山”字需要$(5n+2)$枚棋子。由$5n+2=52$，得$n=10$。

7. 如图所示的两台天平保持平衡.已知每块巧克力的质量相等,且每个果冻的质量也相等,则每个果冻的质量为 ()

A. 40g
B. 35g
C. 30g
D. 20g

答案： C 解析：设每个果冻的质量为xg，则每块巧克力的质量为$(50-x)g$。根据题意，得$2x=3(50-x)$。解这个方程，得$x=30$。因此，每个果冻的质量为30g。

8. (分类讨论思想)(2024·威海)如图,在数轴上,动点A从表示-3的点出发,以1个单位长度/秒的速度沿着数轴的正方向运动.同时,动点B从表示12的点出发,以2个单位长度/秒的速度沿着数轴的负方向运动.经过______秒,点A,B之间的距离等于3个单位长度.

答案： 4或6 解析：设经过x秒，点A，B之间的距离等于3个单位长度。根据题意，得$|(-3+x)-(12-2x)|=3$，解得$x=4$或6。

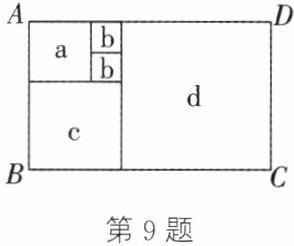
9. (新考向·数学文化)如果一个长方形内部能用一些正方形铺满,既不重叠,又无缝隙,那么就称它为“优美长方形”.如图,“优美长方形”ABCD的周长为26,试求出正方形d的边长.

答案： 设正方形b的边长为x，则正方形a的边长为2x，正方形c的边长为3x，正方形d的边长为5x。根据题意，得$2(3x+5x+5x)=26$。解这个方程，得$x=1$，此时$5x=5\times1=5$。答：正方形d的边长为5

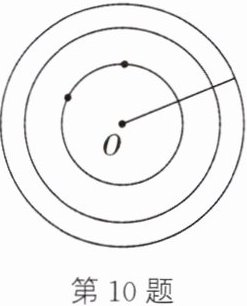
10. (新情境·现实生活)(2023·娄底)如图,若干名同学参加课后社团——舞蹈活动,一次排练中,先到的n名同学均匀排成一个以点O为圆心,r为半径的圆圈(每名同学对应圆周上一个点),又来了两名同学,先到的同学都沿各自所在半径往后移a米,再左右调整位置,使这$(n+2)$名同学之间的距离与原来n名同学之间的距离(即在圆周上两人之间的圆弧的长)相等.这$(n+2)$名同学排成圆圈后,又有一名同学要加入队伍,重复前面的操作,则每人须往后移______米(请用含a的代数式表示),才能使得这$(n+3)$名同学之间的距离与原来n名同学之间的距离相等.

答案： $\frac{a}{2}$ 解析：原来n名同学之间的距离为$\frac{2\pi r}{n}$，$(n+2)$名同学之间的距离为$\frac{2\pi(r+a)}{n+2}$。根据题意，得$\frac{2\pi r}{n}=\frac{2\pi(r+a)}{n+2}$。整理，得$2r=na$，即$\frac{r}{n}=\frac{a}{2}$。设又有一名同学要加入队伍时，每人须向后移x米，这$(n+3)$名同学之间的距离为$\frac{2\pi(r+a+x)}{n+3}$。根据题意，得$\frac{2\pi(r+a+x)}{n+3}=\frac{2\pi r}{n}$。整理，得$x=\frac{3r}{n}-a$。将$\frac{r}{n}=\frac{a}{2}$代入，得$x=\frac{3r}{n}-a=3\times\frac{a}{2}-a=\frac{a}{2}$。