《2025年通城学典课时作业本七年级数学上册苏科版江苏专版》

13. (2023·杭州)已知数轴上的点A,B分别表示数a,b,其中$-1\lt a＜0,0\lt b＜1$.若$a×b= c$,数c在数轴上用点C表示,则点A,B,C在数轴上的位置可能是()

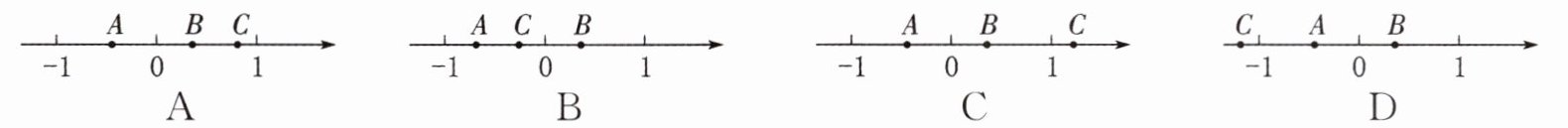
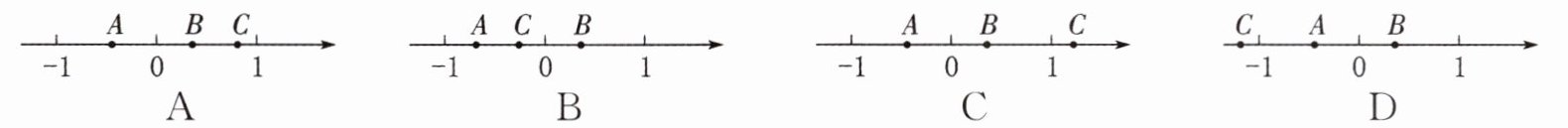
A.
B.
C.
D.

答案： B

14. 在$3,-|-3.5|,-[-(-3\frac {2}{5})],0$这四个数中,最小的数为______.

答案： $-|-3.5|$

15. 如果一个数是6,另一个数比6的相反数小3,那么这两个数的差的绝对值是______.

答案： 15

16. (1)请你在如图所示的数轴上表示下列有理数:$-\frac {1}{2},|-2.5|,0,-2^{2},-(-4);$
(2)将上述各数用“＞”连接.

答案：

(1) 如图所示
(2) $-(-4)＞|-2.5|＞0＞-\frac{1}{2}＞-2^{2}$

17. 计算:
(1)$-3-4+10-11+2;$
(2)$-2^{4}×(1-\frac {3}{4});$
(3)$(-2)^{3}÷2^{4}-|-\frac {1}{4}|×(-10^{2});$
(4)$2022\frac {1}{31}÷5+522\frac {1}{31}×(-\frac {1}{5});$
(5)$1-(-32)×(\frac {3}{4}-2\frac {1}{2}+1\frac {5}{8});$
(6)$(-1)^{201}-\frac {1}{6}×[2×(-1)^{2}-(-3)^{3}].$

答案：
(1) -6
(2) -4
(3) $\frac{49}{2}$
(4) 300
(5) -3
(6) $-\frac{35}{6}$