《2025年通城学典课时作业本七年级数学上册苏科版江苏专版》

18. (新考向·跨学科)(2023·河北)光年是天文学上的一种距离单位,一光年是指光在一年内走过的路程,约等于$9.46×10^{12}km$,则下列结论正确的是()
A. $9.46×10^{12}-10= 9.46×10^{11}$
B. $9.46×10^{12}-0.46= 9×10^{12}$
C. $9.46×10^{12}$是一个十二位数
D. $9.46×10^{12}$是一个十三位数

答案： D

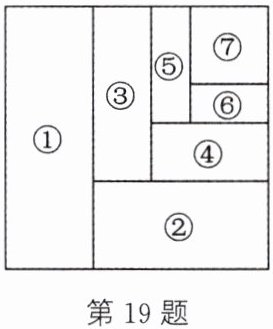
19. (数形结合思想)如图,将一张边长为1的正方形纸片分割成7个图形,图形①的面积是正方形纸片面积的$\frac {1}{3}$,图形②的面积是图形①面积的2倍的$\frac {1}{3}$,图形③的面积是图形②面积的2倍的$\frac {1}{3}$……图形⑥的面积是图形⑤面积的2倍的$\frac {1}{3}$,图形⑦的面积是图形⑥面积的2倍.计算$\frac {1}{3}+\frac {2}{9}+\frac {4}{27}+... +\frac {2^{5}}{3^{6}}$的结果为()

A. $\frac {665}{729}$
B. $\frac {64}{729}$
C. $\frac {179}{243}$
D. $\frac {64}{243}$

答案： A 解析: 根据题意, 得 $\frac{1}{3}+\frac{2}{9}+\frac{4}{27}+... +\frac{2^{5}}{3^{6}}$ 恰好为图形①~⑥的面积之和, 即为正方形的面积减去图形⑦的面积, 所以原式 $=1-2×\frac{2^{5}}{3^{6}}=1-\frac{64}{729}=\frac{665}{729}$。

20. 已知$|a|= 3,|b|= 4$,且$a\lt b$,则$a-b$的值为______.

答案： -1 或 -7

21. 给出下列有理数:-5,1,-3,5,-2,0.从中任意抽取三个数进行相加或者相乘.
(1)和的最大值为______,和的最小值为______;
(2)积的最大值为______,积的最小值为______.

答案：
(1) 6 -10
(2) 75 -30

22. (新考法·新定义题)规定新运算:对于任意有理数a,b,都有$a\oplus b= a×(a-b)+1$.等式右边是通常的加法、减法及乘法运算,如$2\oplus 5= 2×(2-5)+1= 2×(-3)+1= -6+1= -5$.若$|x+2|+(y-3)^{2}= 0$,求$x\oplus y$的值.

答案： 因为 $|x+2|+(y-3)^{2}=0$, 所以 $|x+2|=0$, $(y-3)^{2}=0$。所以 $x+2=0$, $y-3=0$, 即 $x=-2$, $y=3$。所以 $x\oplus y=(-2)\oplus 3=(-2)×(-2 - 3)+1=(-2)×(-5)+1=10 + 1=11$

23. (新情境·现实生活)某检修小组从A地出发,在东西走向的马路上检修线路.如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下表(单位:km):

(1)在第几次记录时距离A地最远?此时距离A地多少千米?
(2)若每千米耗油0.25升,每升汽油7元,则该检修小组工作一天回到A地需汽油费多少元?

答案：
(1) 第一次距离 A 地 $|-3|=3(km)$, 第二次距离 A 地 $|-3+8|=5(km)$, 第三次距离 A 地 $|-3+8-9|=4(km)$, 第四次距离 A 地 $|-3+8-9+10|=6(km)$, 第五次距离 A 地 $|-3+8-9+10+4|=10(km)$, 第六次距离 A 地 $|-3+8-9+10+4-6|=4(km)$, 第七次距离 A 地 $|-3+8-9+10+4-6-2|=2(km)$。所以第五次记录时距离 A 地最远, 此时距离 A 地 10 km
(2) 因为 $|-3|+|+8|+|-9|+|+10|+|+4|+|-6|+|-2|+2=44(km)$, 所以 $44×0.25×7=77$(元)。所以该检修小组工作一天回到 A 地需汽油费 77 元