《2025年通城学典课时作业本七年级数学上册苏科版江苏专版》

7. (教材 P150 习题第 3 题变式)如图所示的正方体的表面展开图为 ()

答案： A

8. (2024·绵阳改编)如图所示为一些几何体的表面展开图,请你在下列横线上分别写出相应几何体的名称.

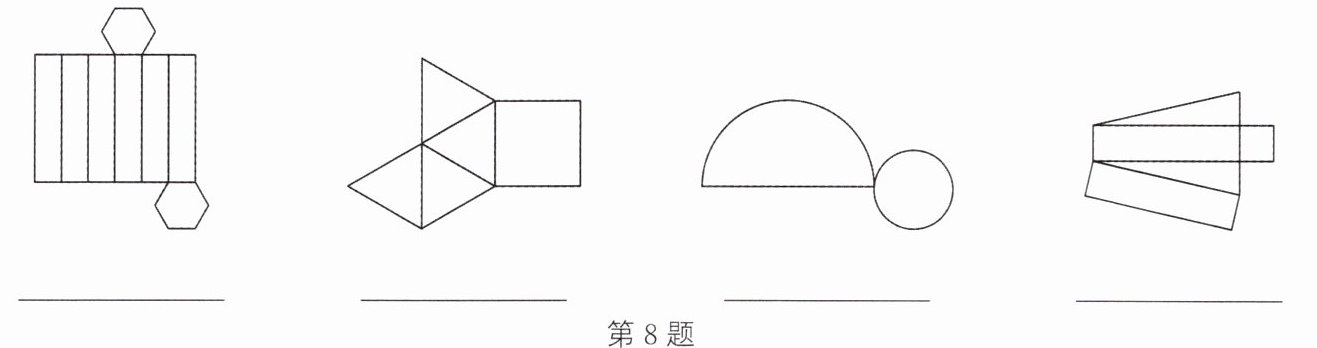
答案： 六棱柱 四棱锥 圆锥 三棱柱

9. 如图所示为一个几何体的表面展开图.
(1) 将它折叠能得到的几何体名称是____;
(2) 若要把这个几何体重新展开,则最少需要剪开____条棱.

答案：
(1) 三棱柱
(2) 5

10. 根据如图所示的图形间的面积关系,在横线上填上适当的代数式,使等式成立:
$ (a - b)^2 = a^2 - 2ab + $____.

答案： $b^{2}$

11. 如图,一个长方体的表面展开图中四边形 $ ABCD $ 是正方形,则根据图中数据可得原长方体的表面积为____ $ cm^2 $.

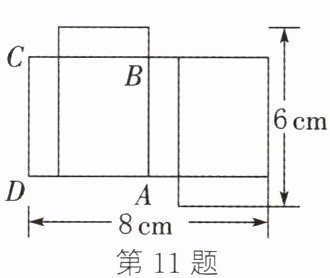
答案：
38 解析：如图，根据长方体的特征，得 $AD = AE = 8÷2 = 4(cm)$。因为四边形 $ABCD$ 是正方形，所以 $CD = AD = 4cm$。所以长方体的高为 $(6 - 4)÷2 = 1(cm)$。所以 $EF = 4 - 1 = 3(cm)$。所以原长方体的表面积为 $(3×4 + 3×1 + 4×1)×2 = 38(cm^{2})$。

12. (教材 P148“探究”变式)如图,由图①、图②和图③中小正方形个数的关系,得到 $ 1^3 + 2^3 = (1 + 2)^2 = 3^2 $.类似地,继续结合图形验证你的猜想,并应用其蕴含的规律求 $ 1^3 + 2^3 + 3^3 + … + 100^3 $ 的值(结果保留幂的形式).

答案： 从所给图形可知，$1^{3} + 2^{3} = (1 + 2)^{2} = 3^{2}$，类似地，可得 $1^{3} + 2^{3} + 3^{3} = (1 + 2 + 3)^{2} = 6^{2}$，$1^{3} + 2^{3} + 3^{3} + 4^{3} = (1 + 2 + 3 + 4)^{2} = 10^{2}$，$\cdots$，所以 $1^{3} + 2^{3} + 3^{3} + \cdots + n^{3} = (1 + 2 + 3 + \cdots + n)^{2}$（$n$ 是正整数）。当 $n = 100$ 时，$1^{3} + 2^{3} + 3^{3} + \cdots + 100^{3} = (1 + 2 + 3 + \cdots + 100)^{2} = 5050^{2}$