《2025年通城学典课时作业本七年级数学上册苏科版江苏专版》

13. 将下列各数填在如图所示的相应的圈内：
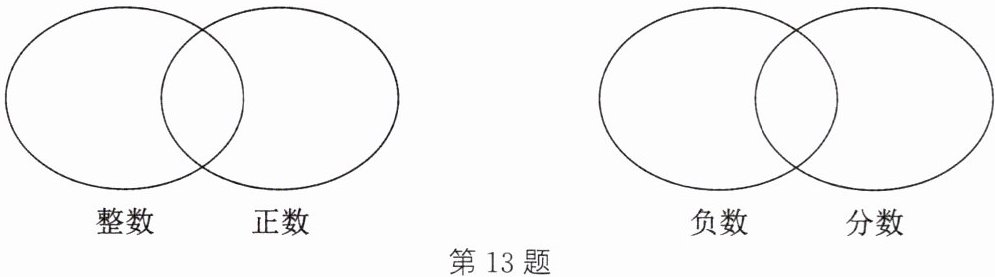
$-3,+6,0,15\%,\frac {22}{7},-303,0.22222… ,-1.8,-\frac {π}{2}$。

答案：
如图所示

14. 计算：
(1)$(-3.9)+(-5.4)+(-1.1)+(+5.4)$；
(2)$-99\frac {81}{82}÷\frac {1}{41}$；
(3)$(-\frac {1}{24})÷(\frac {3}{4}-\frac {5}{6}+\frac {2}{3})$；
(4)$-7÷\frac {7}{22}+26×(-\frac {22}{7})-2×3\frac {1}{7}$。

答案：
(1) $-5$
(2) $-4099\frac{1}{2}$
(3) $-\frac{1}{14}$
(4) $-110$

15.(新考法·新定义题)已知有理数$a≠1$,我们把$\frac {1}{1-a}$称为a的差倒数,如2的差倒数是$\frac {1}{1-2}= -1$,$-1的差倒数是\frac {1}{1-(-1)}= \frac {1}{2}$。如果$a_{1}= -3$,$a_{2}是a_{1}$的差倒数,$a_{3}是a_{2}$的差倒数,$a_{4}是a_{3}$的差倒数……依此类推,解答下面的问题：
(1)$a_{2}= $______,$a_{3}= $______,$a_{4}= $______；
(2)求$a_{1}+a_{2}+a_{3}+a_{4}+… +a_{2023}+a_{2024}+a_{2025}+a_{2026}$的值。

答案：
(1) $\frac{1}{4}$ $\frac{4}{3}$ $-3$
(2) 根据$a_{1}=-3$，$a_{2}=\frac{1}{4}$，$a_{3}=\frac{4}{3}$，$a_{4}=-3$，$\cdots$，可知$a_{1}$，$a_{2}$，$a_{3}$，$\cdots$，这列数每三个数为一个循环。因为$2026\div 3=675\cdots \cdots 1$，$a_{1}+a_{2}+a_{3}=-3+\frac{1}{4}+\frac{4}{3}=-\frac{17}{12}$，所以$-\frac{17}{12}\times 675=-\frac{3825}{4}$。所以$a_{1}+a_{2}+a_{3}+a_{4}+\cdots +a_{2023}+a_{2024}+a_{2025}+a_{2026}=-\frac{3825}{4}+(-3)=-\frac{3837}{4}$