第117页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
8. (整体思想)已知$∠α$是锐角,$∠α与∠β$互补,$∠α与∠γ$互余,则$∠β-∠γ$的度数为 ()
A. $45^{\circ }$
B. $60^{\circ }$
C. $90^{\circ }$
D. $180^{\circ }$
A. $45^{\circ }$
B. $60^{\circ }$
C. $90^{\circ }$
D. $180^{\circ }$
答案:
C
9. 若$∠1与∠2$互为补角,且$∠1<∠2$,则$∠1$的余角为 ()
A. $∠1$
B. $∠1+∠2$
C. $\frac {1}{2}(∠1+∠2)$
D. $\frac {1}{2}(∠2-∠1)$
A. $∠1$
B. $∠1+∠2$
C. $\frac {1}{2}(∠1+∠2)$
D. $\frac {1}{2}(∠2-∠1)$
答案:
D 解析:运用特殊值法,不妨设∠1=80°,∠2=100°,则∠1的余角为90°−80°=10°。将∠1=80°,∠2=100°代入四个选项中求值,只有$\frac{1}{2}$(∠2−∠1)的值为10°。
10. 如图,点O在直线AB上,$∠AOC= 53^{\circ }17'28''$,则$∠BOC= $______$^{\circ }$______$'$______$''$.
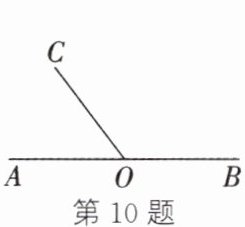

答案:
126 42 32
11. (方程思想)已知$∠1与∠2$互余,$∠1= (6x+8)^{\circ },∠2= (4x-8)^{\circ }$,则$∠1$的度数为______,$∠2$的度数为______.
答案:
62° 28°
12. 如图,$∠ACB= ∠CDB= 90^{\circ }$,则$∠ACD$的余角有______个,它们是______.
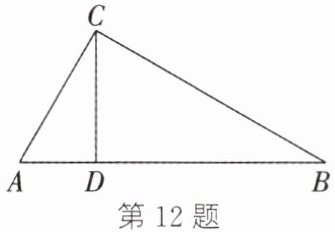

答案:
2 ∠BCD,∠A
13. (新考法·综合与实践)如图,将一张长方形纸片先沿CP折叠,使点A落在点E处,再将纸片的另一角沿PD折叠,使点B落在点F处,且PE与PF在同一条直线上.
(1)$∠APC与∠FPD$互余吗?为什么?
(2)$∠CPF与∠CPB$互补吗?为什么?
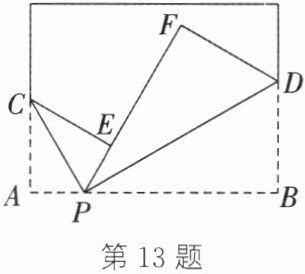
(1)$∠APC与∠FPD$互余吗?为什么?
(2)$∠CPF与∠CPB$互补吗?为什么?

答案:
(1)∠APC与∠FPD互余 由折叠可知,∠APC=∠CPE=$\frac{1}{2}$∠APE,∠BPD=∠FPD=$\frac{1}{2}$∠BPF,所以∠APC+∠FPD=$\frac{1}{2}$∠APE+$\frac{1}{2}$∠BPF=$\frac{1}{2}$(∠APE+∠BPF)=$\frac{1}{2}$∠APB。又因为∠APB=180°,所以∠APC+∠FPD=$\frac{1}{2}$×180°=90°,即∠APC与∠FPD互余 (2)∠CPF与∠CPB互补 由折叠可知,∠CPF=∠CPA,所以∠CPF+∠CPB=∠CPA+∠CPB=∠APB=180°,即∠CPF与∠CPB互补
14. 如图,$∠AOC与∠BOC$互为补角,$∠BOC与∠BOD$互为余角,且$∠BOC= 4∠BOD$.
(1) 求$∠BOC$的度数;
(2) 若$∠COE= ∠AOE$,求$∠BOE$的度数.
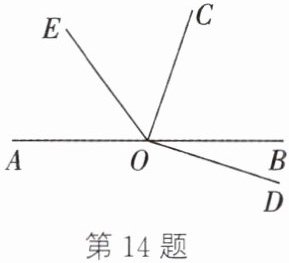
(1) 求$∠BOC$的度数;
(2) 若$∠COE= ∠AOE$,求$∠BOE$的度数.

答案:
(1)因为∠BOC与∠BOD互为余角,所以∠BOC+∠BOD=90°。因为∠BOC=4∠BOD,所以∠BOC=$\frac{4}{5}$×90°=72° (2)因为∠AOC与∠BOC互为补角,所以∠AOC+∠BOC=180°。由(1)知,∠BOC=72°,所以∠AOC=180°−∠BOC=180°−72°=108°。因为∠COE=∠AOE,所以∠COE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×108°=54°。所以∠BOE=∠COE+∠BOC=54°+72°=126°
查看更多完整答案,请扫码查看


