《2025年时习之暑假衔接八年级数学北师大版》

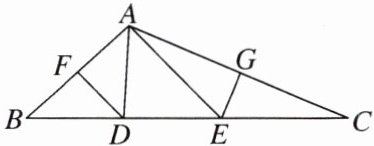
5.如图,在△ABC中,∠BAC= 110°,AB的垂直平分线DF交BC于点D,AC的垂直平分线EG交BC于点E,BC= 10cm。求：
(1)△ADE的周长；
(2)∠DAE的度数。

答案：
(1)
∵DF垂直平分AB，EG垂直平分AC，
∴AD=BD,AE=EC,
∴△ADE的周长=AD+DE+AE=BD+DE+CE=BC=10cm.
(2)
∵AD=BD,AE=CE,
∴∠B=∠BAD,∠C=∠EAC,
∴∠ADE=2∠B,∠AED=2∠C.而∠B+∠C=180°−∠BAC=70°,
∴∠ADE+∠AED=2(∠B+∠C)=140°,
∴∠DAE=180°−140°=40°.

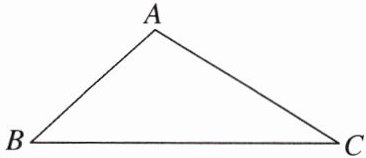
6.下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程。
已知：如图,△ABC。
求作：△ABC中BC边上的高线AD。
作法：①以点B为圆心,BA的长为半径作弧,以点C为圆心,CA的长为半径作弧,两弧在BC下方交于点E；②连接AE交BC于点D,则线段AD是△ABC中BC边上的高线。
根据小东设计的尺规作图过程,完成下列问题：
(1)使用直尺和圆规,补全图形(保留作图痕迹)。

(2)连接BE,CE,完成下面的证明。
证明：∵____= BA,____= CA,
∴点B,C均在线段AE的垂直平分线上(____)(填推理的依据)。
∴BC垂直平分线段AE。
∴线段AD是△ABC中BC边上的高线。

答案：

(1)图形如图所示.
(2)BE　EC　到线段两个端点距离相等的点在线段的垂直平分线上

7.如图是一块三角形的草坪,现要在草坪上建一座凉亭供大家休息,使凉亭到草坪三条边的距离相等,凉亭的位置应选在()

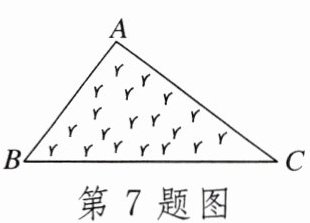
A.△ABC三条中线的交点处
B.△ABC三边的垂直平分线的交点处
C.△ABC三条角平分线的交点处
D.△ABC三条高所在直线的交点处

答案： C

8.如图,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F。若S△ABC= 10,DF= 2,AC= 4,则AB的长是()

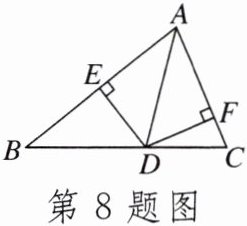
A.2
B.4
C.6
D.8

答案： C

9.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点。若PA= 2,则PQ的最小值为____。

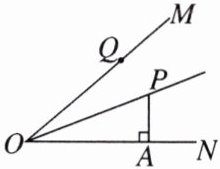
答案： 2

10.如图,AB= AC,BD= CD,DE⊥AB于点E,DF⊥AC于点F。求证：DE= DF。

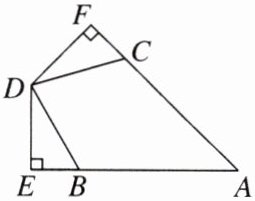
答案： 连接AD,在△ABD和△ACD中，$\begin{cases}AB = AC\\BD = CD\\AD = AD\end{cases}$，
∴△ABD≌△ACD(SSS).
∴∠FAD=∠EAD.又
∵DE⊥AB,DF⊥AC,
∴DE=DF.