《2025年时习之暑假衔接八年级数学北师大版》

2. 某社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边。已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%。若设白边的宽为x米,则根据题意可列方程为______。

答案： $ 90\%(2 + 2x)(1 + 2x) = 2 $

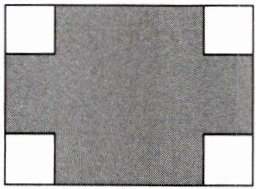
3. 如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求截去的小正方形的边长。

答案： 设截去的小正方形的边长为 $ x $ cm。由题意得 $ 10×8 - 4x^2 = 80\%×10×8 $。解得 $ x_1 = 2 $，$ x_2 = -2 $。经检验，$ x_1 = 2 $ 符合题意，$ x_2 = -2 $ 不符合题意，舍去。$ \therefore x = 2 $。
答：所截去的小正方形的边长为 2 cm。

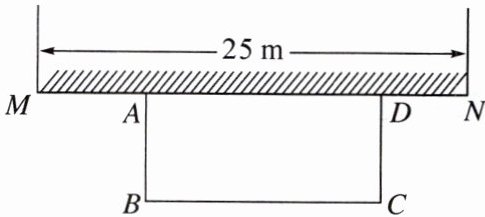
4. 如图,某中学准备在校园里利用一段围墙,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m)。现已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为$300m^2。$

答案： 设 $ AB = x $ m，则 $ BC = (50 - 2x) $ m。根据题意可得 $ x(50 - 2x) = 300 $，解得 $ x_1 = 10 $，$ x_2 = 15 $。当 $ x = 10 $ 时，$ BC = 50 - 2×10 = 30(m) ＞ 25m $，故 $ x_1 = 10 $ 不合题意，舍去；当 $ x = 15 $ 时，$ BC = 50 - 2×15 = 20(m) ＜ 25m $，符合题意。
答：可以砌成长为 20 m，宽为 15 m 的矩形花园。

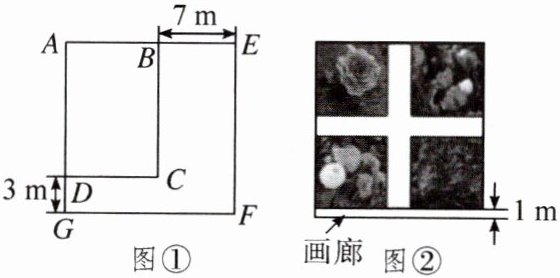
5. 为了丰富学生的课余生活,培养学生德智体美劳全面发展,某校成立了众多种类的学生社团。其中勤学社团会定期组织学生参与农耕劳作,感受劳动之美。如图①,在生态大棚中有一块面积为$45m^2$的矩形空地ABCD,计划将矩形空地的一边增加7m,另一边增加3m,构成一个正方形区域AEFG,作为学生栽种鲜花的劳动教育基地。
(1)求正方形区域AEFG的边长。
(2)在实际建造时,从校园美观和实用的角度考虑,按图②的方式进行改造,先在图②中所得正方形区域内的一侧建成1m宽的画廊,再在余下地方建成宽度相等的两条垂直小道后,其余地方栽种鲜花。如果栽种鲜花区域的面积为$90m^2,$求小道的宽度。

答案：
(1) 设正方形区域 $ AEFG $ 的边长为 $ x $ m，则 $ AB = (x - 7) $ m，$ AD = (x - 3) $ m，由题意得 $ (x - 7)(x - 3) = 45 $，解得 $ x = 12 $ 或 $ x = -2 $（舍去）。$ \therefore $ 正方形区域 $ AEFG $ 的边长为 12 m。
(2) 设小道的宽度为 $ x $ m，则栽种鲜花的区域长为 $ (12 - x) $ m，宽为 $ (12 - 1 - x) $ m，由题意得 $ (12 - x)(12 - 1 - x) = 90 $，解得 $ x_1 = 2 $，$ x_2 = 21 $（不合题意，舍去）。
答：小道的宽度为 2 m。