《2025年时习之暑假衔接八年级数学北师大版》

7. 解不等式组$\left\{\begin{array}{l} 2x-1＞x+1,\\ x+8＞4x-4,\end{array}\right. $并将其解集在数轴上表示出来.

答案： $2＜x＜4$,数轴表示略.

8. 某隧道全长9公里,有一辆汽车以每小时60公里到80公里之间的速度通过该隧道.下列可能是该车通过隧道所用的时间是()
A. 6分钟
B. 8分钟
C. 10分钟
D. 12分钟

答案： B

9. 某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元；本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1) 求每辆A型车和B型车的售价各为多少元；
(2) 甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元,则有哪几种购车方案？

答案：
(1)设每辆A 型车和B 型车的售价各为x 万元与y 万元,则依题意可得$\left\{\begin{array}{l} x+3y=96,\\ 2x+y=62,\end{array}\right. $解得$\left\{\begin{array}{l} x=18,\\ y=26.\end{array}\right. $
答:每辆A 型车和B 型车的售价分别为18 万元与26 万元.
(2)设购买A 型车z 辆,则$\left\{\begin{array}{l} 18z+26(6-z)≥130,\\ 18z+26(6-z)≤140,\end{array}\right. $解得$2≤z≤3\frac {1}{4}$.因为z 为正整数,所以z 取2,3.故共有两种购车方案:方案一是购买2 辆A 型车,4 辆B 型车;方案二是购买3 辆A 型车,3 辆B 型车.

1. 不同种类的药品的保存温度有区别.已知甲药品的保存温度为$2^{\circ }C\sim 8^{\circ }C$,乙药品的保存温度为$5^{\circ }C\sim 15^{\circ }C$.若将甲、乙两种可以共同存放的药品放在一起保存,则下列能符合要求的温度是()
A. $2^{\circ }C$
B. $4^{\circ }C$
C. $6^{\circ }C$
D. $10^{\circ }C$

答案： C

2. 不等式组$\left\{\begin{array}{l} \frac {1}{3}x+1＞0,\\ 2-x\geqslant 0\end{array}\right. $的解集在数轴上可表示为()

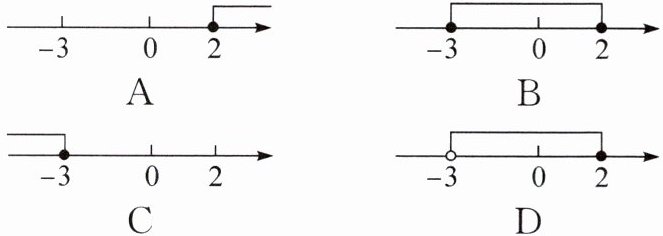
答案： D

3. 在平面直角坐标系内,点$P(2x-6,x-5)$在第四象限,则x的取值范围为()
A. $3＜x＜5$
B. $-3＜x＜5$
C. $-5＜x＜3$
D. $-5＜x＜-3$

答案： A

4. 不等式组$\left\{\begin{array}{l} 3x+6\geqslant 0,\\ 4-2x＞0\end{array}\right. $的所有整数解的和为____.

答案： -2

5. 解不等式组：$\left\{\begin{array}{l} 3x+4\geqslant x-2,\\ \frac {2x+1}{3}-\frac {x-1}{2}＜1\end{array}\right. $

答案： $-3≤x＜1$.

6. 已知关于x,y的方程组$\left\{\begin{array}{l} x-2y= m①,\\ 2x+3y= 2m+4②\end{array}\right. 的解满足不等式组\left\{\begin{array}{l} 3x+y\leqslant 0,\\ x+5y＞0,\end{array}\right. $求满足条件的m的整数值.

答案： ①+②,得$3x+y=3m+4$③,②-①,得$x+5y=m+4$④,将③④代入不等式组中得$\left\{\begin{array}{l} 3m+4≤0,\\ m+4＞0,\end{array}\right. $解得$-4＜m≤-\frac {4}{3}$,故满足条件的m 的整数值为-3,-2.