《2025年时习之暑假衔接八年级数学北师大版》

6.如图,将$Rt\triangle ABC沿直角边AB向右平移\sqrt{3}个单位得到Rt\triangle DEF$.若$AC= 4$,$∠ABC= 90^{\circ}$,$∠CAB= 30^{\circ}$,求图中阴影部分的面积.

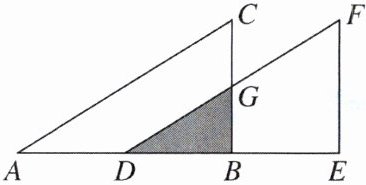
答案：
∵$\angle ABC = 90^{\circ}$，$\angle CAB = 30^{\circ}$，$AC = 4$，
∴$BC = \frac{1}{2}AC = 2$，
∴$AB = \sqrt{AC^{2}-BC^{2}} = 2\sqrt{3}$.又
∵$AD = \sqrt{3}$，
∴$BD = 2\sqrt{3}-\sqrt{3} = \sqrt{3}$.易得$BG = 1$.
∴$S_{\triangle DBG} = \frac{\sqrt{3}}{2}$.

7.(手拉手模型)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,那么把它们的底角顶点连接起来则形成一组全等的三角形.小明把具有这个规律的图形称为“手拉手”图形.
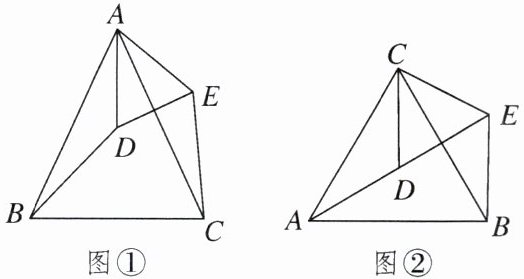
(1)[问题发现]如图①,若$\triangle ABC和\triangle ADE均是顶角为40^{\circ}$的等腰三角形,$BC$,$DE$分别是底边,可以由____(三角形全等判定原理),得$\triangle ABD≌\triangle ACE$,进而得到$BD= CE$;
(2)[拓展探究]如图②,若$\triangle ABC和\triangle CDE$均为等边三角形,点$A$,$D$,$E$在同一条直线上,连接$BE$,求$∠AEB$的度数.

答案：
(1)SAS
(2)
∵$\triangle ABC$和$\triangle CDE$均是等边三角形，
∴$CA = CB$，$CD = CE$，$\angle ACB = \angle DCE = \angle CDE = \angle CED = 60^{\circ}$.
∴$\angle ACB - \angle BCD = \angle DCE - \angle BCD$.
∴$\angle ACD = \angle BCE$.
∴$\triangle ACD\cong\triangle BCE(SAS)$.
∴$AD = BE$，$\angle ADC = \angle BEC$.
∵$\angle CDE = 60^{\circ}$，
∴$\angle BEC = \angle ADC = 180^{\circ}-\angle CDE = 120^{\circ}$.
∵$\angle CED = 60^{\circ}$，
∴$\angle AEB = \angle BEC - \angle CED = 60^{\circ}$.

8.(半角模型)如图①,四边形$ABCD$是正方形,$E$,$F分别在边BC和CD$上,且$∠EAF= 45^{\circ}$(此时$∠EAF= \frac{1}{2}∠BAD$),我们把这种模型称为“半角模型”.小明为了解决线段$EF$,$BE$,$DF$之间的关系,将$\triangle ADF绕点A顺时针旋转90^{\circ}$后(如图②)解决了这个问题.

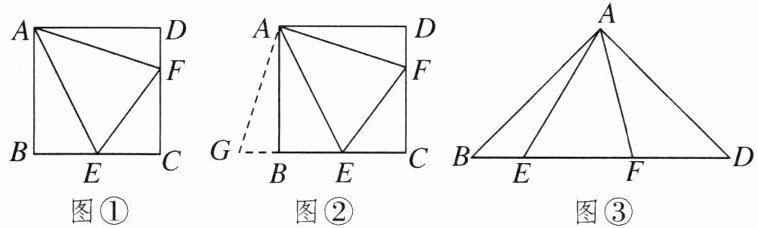
(1)写出线段$EF$,$BE$,$DF$之间的数量关系,并说明理由;
(2)如图③,等腰直角三角形$ABD$中,$∠BAD= 90^{\circ}$,$AB= AD$,点$E$,$F在边BD$上,且$∠EAF= 45^{\circ}$,请写出$EF$,$BE$,$DF$之间的数量关系,并说明理由.

答案：

(1)$EF = BE + DF$.理由如下：
∵四边形$ABCD$是正方形，
∴$AB = AD$，$\angle D = \angle ABE = \angle DAB = 90^{\circ}$.
∵$\triangle ADF$绕点$A$顺时针旋转$90^{\circ}$后得到$\triangle ABG$，
∴$AF = AG$，$BG = DF$，$\angle ABG = \angle D = 90^{\circ}$，$\angle DAF = \angle GAB$.
∴$\angle ABG + \angle ABE = 180^{\circ}$，即点$G$在$EB$的延长线上.
∵$\angle EAF = 45^{\circ}$，$\angle DAB = 90^{\circ}$，
∴$\angle BAE + \angle DAF = 45^{\circ}$.
∴$\angle BAE + \angle GAB = 45^{\circ}$，即$\angle EAF = \angle GAE = 45^{\circ}$.
∵$AF = AG$，$AE = AE$，
∴$\triangle AFE\cong\triangle AGE(SAS)$.
∴$EF = GE = GB + BE$，即$EF = BE + DF$.故线段$EF$，$BE$，$DF$之间的数量关系为$EF = BE + DF$.
(2)$EF^{2} = BE^{2} + DF^{2}$.理由如下：
∵$\angle BAD = 90^{\circ}$，$AB = AD$，
∴$\angle ABE = \angle D = 45^{\circ}$.如图，把$\triangle ADF$绕点$A$顺时针旋转$90^{\circ}$后得到$\triangle ABG$，则$AF = AG$，$BG = DF$，$\angle ABG = \angle D = 45^{\circ}$，$\angle DAF = \angle GAB$.
∴$\angle ABG + \angle ABE = 45^{\circ}+45^{\circ} = 90^{\circ}$，即$\angle GBE = 90^{\circ}$.
∴$GE^{2} = BE^{2} + BG^{2} = BE^{2} + DF^{2}$.
∵$\angle EAF = 45^{\circ}$，$\angle DAB = 90^{\circ}$，
∴$\angle BAE + \angle DAF = 45^{\circ}$.
∴$\angle BAE + \angle GAB = 45^{\circ}$，即$\angle EAF = \angle GAE = 45^{\circ}$.
∵$AF = AG$，$AE = AE$，
∴$\triangle AFE\cong\triangle AGE(SAS)$.
∴$EF = GE$.
∴$EF^{2} = BE^{2} + DF^{2}$.