《2025年时习之暑假衔接八年级数学北师大版》

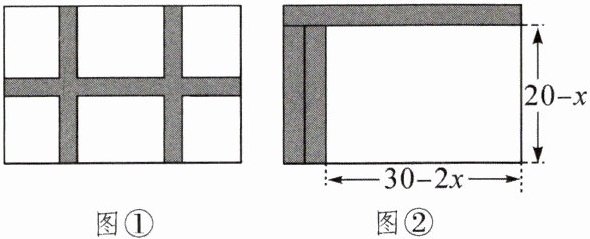
例 为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长为30m,宽为20m的长方形空地建成一个矩形花园。要求在花园中修两条纵向平行和一条横向的小道,剩余的地方种植花草,如图①所示。如果要使种植花草的面积为$532m^2,$那么小道的宽度应为多少？(注：所有小道的宽度相等)

答案：

导析：根据图形平移的性质,将原图中的小道平移到如图②所示的位置后,小道的面积不变,种植花草的面积也不会变。设小道的宽度为x m,根据矩形的面积公式列一元二次方程解答。

解答：设小道的宽度为x m。

根据题意,得(30-2x)(20-x)= 532。

整理,得$x^2-35x+34= 0。$

解得$x_1= 1,x_2= 34。$

∵34＞30(不合题意,舍去),

∴x= 1。

答：小道的宽度应为1m。

方法归纳：运用一元二次方程解与面积有关的应用题时,要注意联想图形中有关的几何定理、面积和体积的公式,充分将数与形结合起来。求得方程的根时,也要注意判断方程的根是否符合实际问题。

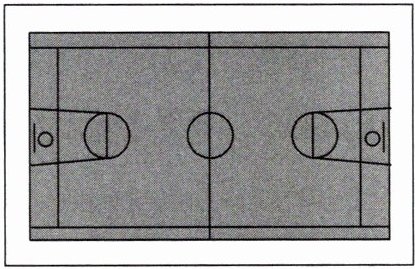
某初中学校要新建一块篮球场地(如图所示),要求：①篮球场地的长和宽分别为28米和16米；②在篮球场地四周修建宽度相等的安全区域；③篮球场地及安全区域的总面积为640平方米。求安全区域的宽度。

答案： 设安全区域的宽度为 $ x $ 米，则 $ (28 + 2x)(16 + 2x) = 640 $，解得 $ x_1 = 2 $，$ x_2 = -24 $（舍去）。
答：安全区域的宽度为 2 米。

1. 用一根10米长的铝材制成一个矩形窗框,使它的面积为6平方米。若设它的一条边长为x米,则根据题意可列出关于x的方程为()
A. x(5+x)= 6
B. x(5-x)= 6
C. x(10-x)= 6
D. x(10-2x)= 6

答案： B