《2025年时习之暑假衔接八年级数学北师大版》

1. 等腰三角形补充下列条件后,仍不一定成为等边三角形的是()
A. 有一个内角是$60^{\circ }$
B. 有一个外角是$120^{\circ }$
C. 有两个角相等
D. 腰长与底边长相等

答案： C

2. 如图,在$\triangle ABC$中,点$D在BC$上,$AB= AD= DC$,$∠B= 70^{\circ }$,则$∠C$的度数为()


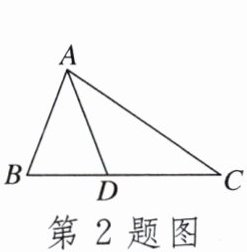
A.$30^{\circ }$
B.$35^{\circ }$
C.$40^{\circ }$
D.$45^{\circ }$

答案： B

3. 如图,在$\triangle ABC$中,$AB= AC$,$AD⊥BC于点D$．若$AB= 6$,$CD= 4$,则$\triangle ABC$的周长是____．

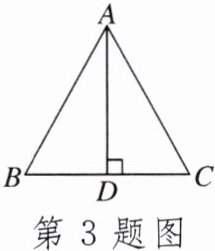
答案： 20

4. 如图,$AD是等边三角形ABC$的中线,点$E是AC$上一点,且$AD= AE$,则$∠EDC= $____$^{\circ }$．

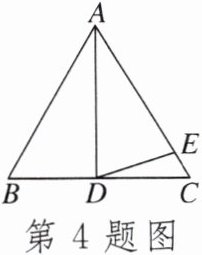
答案： 15

5. 如图,等边三角形$ABC的周长为12cm$,$DC// AB$,$AD⊥CD于点D$,则$CD= $____cm．

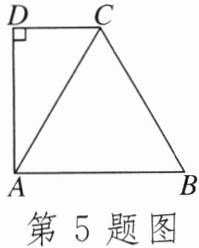
答案： 2

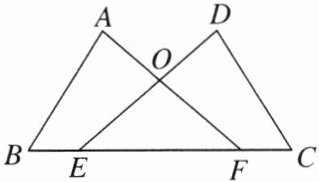
6. 如图,点$E$,$F在BC$上,$BE= CF$,$∠A= ∠D$,$∠B= ∠C$,$AF与DE交于点O$．
(1)求证：$AB= DC$；
(2)试判断$\triangle OEF$的形状,并说明理由．

答案：
(1)$\because BE=FC,\therefore BE+EF=FC+EF$,即$BF=CE.$
又$\because ∠A=∠D,∠B=∠C,\therefore △ABF\cong △DCE.\therefore AB=DC.$
(2)$△OEF$为等腰三角形,理由如下:$\because △ABF\cong △DCE,$
$\therefore ∠AFB=∠DEC.\therefore △OEF$为等腰三角形.

三角形面积公式
在小学我们就学习了求三角形面积的公式,三角形的面积$=\frac {1}{2}×底×$高．
古希腊的几何学家海伦(Heron,约公元50年),在数学史上以解决几何测量问题而闻名,在他的著作《度量》一书中,给出了三角形面积的计算公式——海伦公式：如果一个三角形的三边长分别为$a$,$b$,$c$,记$p= \frac {a+b+c}{2}$,那么三角形的面积为$S= \sqrt {p(p-a)(p-b)(p-c)}$．
我国南宋时期数学家秦九韶(约1202—约1261),曾提出利用三角形的三边求面积的秦九韶公式：$S= \sqrt {\frac {1}{4}[a^{2}b^{2}-(\frac {a^{2}+b^{2}-c^{2}}{2})^{2}]}$．
[思考应用]已知一个三角形的三边长分别为4,5,6,求这个三角形的面积．

答案：

解：由题意得​$p=\frac {a + b + c}2=\frac {4 + 5 + 6}2=\frac {15}2​$

∴​$S=\sqrt {p(p - a)(p - b)(p - c)}=\sqrt {\frac {15}2×(\frac {15}2-4)×(\frac {15}2-5)×(\frac {15}2-6)}=\frac {15\sqrt 7}4​$