2025年时习之暑假衔接八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
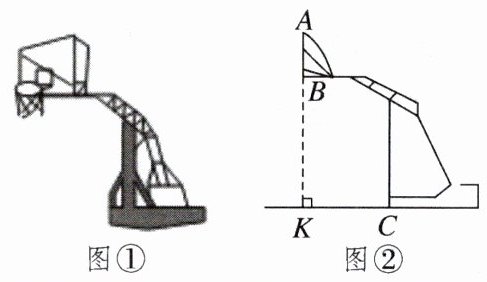
图①是某校篮球架实物图,图②是篮球架的侧面示意图,篮板侧边AB垂直于地面。八年级的“综合与实践”兴趣组将分成两个小组开展测量篮球架篮板AB长度的实践活动。在不便于直接测量的情况下,两个小组设计了如下测量方案:
|课题|测量篮球架篮板AB长度|
|----|----|
|组名|第一组|第二组|
|成员|组长:小明 组员:小亮,小丽,小辉|组长:小红 组员:小玲,小文,小海|
|工具|竹竿,皮尺,测角仪|竹竿,皮尺|
|测量示意图| |
| |
|
|测量方法|将竹竿HE垂直固定在地面CD上,小明从竹竿上的F点处观察篮板底部B点,用测角仪测量视线FB与竹竿HE的夹角∠HFB的度数,接着将观察点沿着竹竿向上移动到G点,使得从G点观察篮板顶部A点的视线GA与竹竿HE的夹角∠HGA的度数恰好等于∠HFB的度数,在竹竿上标注G点的位置,测量GF的长度。|将一根竹竿靠在篮板AB上,竹竿的一端与篮板顶部A点重合,竹竿另一端点落在地面K点正前方的点M处,在地面上标注M点的位置,接着将竹竿与A点重合的一端沿着篮板下滑,直到该端点与篮板底部B点重合,此时,另一端点落在地面K点正前方的点N处,在地面上标注N点的位置,测量KM和KN的长度。|
|测量数据|测量项目|数值|测量项目|数值|
||∠HFB的度数|48°|竹竿的长度||
||∠HGA的度数|48°|KM的长度|3|
||GF的长度|1米|KN的长度|4|
(1)小明说:“GF的长度就是篮板AB的长度。”你认为小明的说法是否正确,并说明理由;
(2)第二小组记录的测量数据中“竹竿长度”的数值不小心被墨水污染后看不清楚,请你结合两个小组记录的测量数据计算第二小组使用的竹竿长度。

|课题|测量篮球架篮板AB长度|
|----|----|
|组名|第一组|第二组|
|成员|组长:小明 组员:小亮,小丽,小辉|组长:小红 组员:小玲,小文,小海|
|工具|竹竿,皮尺,测角仪|竹竿,皮尺|
|测量示意图|
 |
| |
||测量方法|将竹竿HE垂直固定在地面CD上,小明从竹竿上的F点处观察篮板底部B点,用测角仪测量视线FB与竹竿HE的夹角∠HFB的度数,接着将观察点沿着竹竿向上移动到G点,使得从G点观察篮板顶部A点的视线GA与竹竿HE的夹角∠HGA的度数恰好等于∠HFB的度数,在竹竿上标注G点的位置,测量GF的长度。|将一根竹竿靠在篮板AB上,竹竿的一端与篮板顶部A点重合,竹竿另一端点落在地面K点正前方的点M处,在地面上标注M点的位置,接着将竹竿与A点重合的一端沿着篮板下滑,直到该端点与篮板底部B点重合,此时,另一端点落在地面K点正前方的点N处,在地面上标注N点的位置,测量KM和KN的长度。|
|测量数据|测量项目|数值|测量项目|数值|
||∠HFB的度数|48°|竹竿的长度||
||∠HGA的度数|48°|KM的长度|3|
||GF的长度|1米|KN的长度|4|
(1)小明说:“GF的长度就是篮板AB的长度。”你认为小明的说法是否正确,并说明理由;
(2)第二小组记录的测量数据中“竹竿长度”的数值不小心被墨水污染后看不清楚,请你结合两个小组记录的测量数据计算第二小组使用的竹竿长度。
答案:
(1)我认为小明的说法正确.理由:$\because HE\perp CD$,$AB\perp CD$,$\therefore \angle HEC=\angle AKC=90^{\circ}$.$\therefore AB// GF$.$\because \angle HGA=\angle HFB$,$\therefore AG// BF$.$\therefore$四边形$AGFB$是平行四边形.$\therefore GF=AB=1$米.$\therefore GF$的长度就是篮板$AB$的长度.
(2)由题意得$AM=BN$,$AB=1$米.设$BK=x$米,$\therefore AK=AB+BK=(x+1)$米.在$Rt\triangle AMK$中,$KM=3$米,$\therefore AM^{2}=AK^{2}+KM^{2}=(x+1)^{2}+9$.在$Rt\triangle BNK$中,$KN=4$米,$\therefore BN^{2}=BK^{2}+KN^{2}=x^{2}+16$.$\therefore (x+1)^{2}+9=x^{2}+16$,解得$x=3$.$\therefore BN^{2}=x^{2}+16=25$.$\therefore BN=5$或$BN=-5$(舍去).$\therefore$第二小组使用的竹竿长度为$5$米.
(1)我认为小明的说法正确.理由:$\because HE\perp CD$,$AB\perp CD$,$\therefore \angle HEC=\angle AKC=90^{\circ}$.$\therefore AB// GF$.$\because \angle HGA=\angle HFB$,$\therefore AG// BF$.$\therefore$四边形$AGFB$是平行四边形.$\therefore GF=AB=1$米.$\therefore GF$的长度就是篮板$AB$的长度.
(2)由题意得$AM=BN$,$AB=1$米.设$BK=x$米,$\therefore AK=AB+BK=(x+1)$米.在$Rt\triangle AMK$中,$KM=3$米,$\therefore AM^{2}=AK^{2}+KM^{2}=(x+1)^{2}+9$.在$Rt\triangle BNK$中,$KN=4$米,$\therefore BN^{2}=BK^{2}+KN^{2}=x^{2}+16$.$\therefore (x+1)^{2}+9=x^{2}+16$,解得$x=3$.$\therefore BN^{2}=x^{2}+16=25$.$\therefore BN=5$或$BN=-5$(舍去).$\therefore$第二小组使用的竹竿长度为$5$米.
查看更多完整答案,请扫码查看


