《2025年时习之暑假衔接八年级数学北师大版》

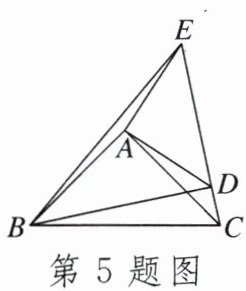
5.如图,在$\triangle ABC$,$\triangle ADE$中,$\angle BAC = \angle DAE = 90^{\circ}$,$AB = AC$,$AD = AE$,$C$,$D$,$E$三点在同一条直线上,连接$BD$,$BE$,以下四个结论:①$BD = CE$;②$BD \perp CE$;③$\angle ACE + \angle DBC = 45^{\circ}$;④$BE = AD + AB$,其中正确的结论是____(填序号).

答案： 5.①②③

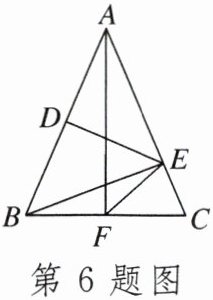
6.如图,在$\triangle ABC$中,$AB = AC$,$DE垂直平分AB$,$BE \perp AC$,点$F为BC$边上一点,且$EF = BF$,则$\angle EFC = $____$^{\circ}$.

答案： 6.45　　点拨:
∵DE垂直平分AB，
∴AE=BE.
∵BE⊥AC,
∴∠BAE=∠ABE=45°.
∵AB=AC,
∴∠ABC=$\frac{1}{2}$×(180°−45°)=67.5°,
∴∠CBE=∠ABC−∠ABE=22.5°.
∵EF=BF,
∴∠BEF=∠CBE=22.5°.
∴∠EFC=180°−∠BFE=2∠CBE=45°.

7.如图,在$\triangle ABC$中,$\angle BAC = 120^{\circ}$,$AB的垂直平分线交AB于点E$,交$BC于点F$,$AC的垂直平分线交AC于点G$,交$BC于点H$.
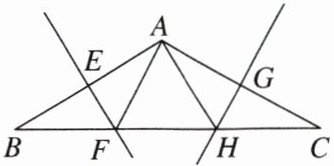
(1)若$AB = AC$,求$\angle FAH$的度数;
(2)若$AB \neq AC$,你能求出$\angle FAH$的度数吗?与(1)的结果是否相同?

答案： 7.
(1)
∵AB=AC,
∴∠B=∠C=$\frac{1}{2}$(180°−∠BAC)=30°.
∵EF垂直平分AB,
∴FA=FB,
∴∠B=∠BAF=30°,同理可得∠C=∠CAH=30°.
∴∠FAH=∠BAC−∠BAF−∠CAH=120°−30°−30°=60°.
(2)能.易证∠B=∠BAF,∠C=∠CAH,
∴∠FAH=∠BAC−∠BAF−∠CAH=∠BAC−(∠B+∠C)=∠BAC−(180°−∠BAC)=240°−180°=60°.与
(1)的结果相同.

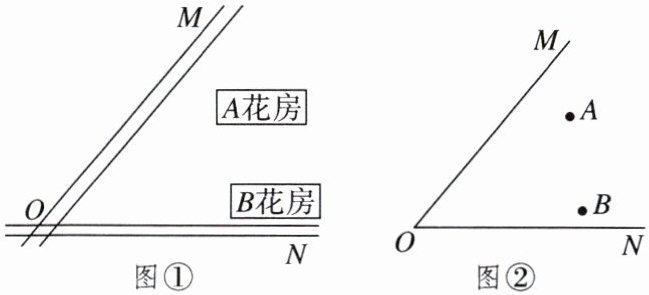
8.如图①,两条交叉马路$OM$,$ON中间区域建有A$,$B$两个温室花房.现要在两条马路$OM$,$ON之间的空场处建鲜花交易中心P$,使得交易中心$P到两条马路OM$,$ON$的距离相等,且到两个温室花房$A$,$B$的距离也相等.如何确定交易中心$P$的位置?如图②,利用尺规作图求作点$P$(不写作法,保留作图痕迹).

答案：
8.如图，点P即为所求.

9.某数学兴趣小组开展了一次活动,过程如下:设$\angle BAC = \theta (0^{\circ} \lt \theta \lt 90^{\circ})$.现把小棒依次摆放在两射线之间,并使小棒两端分别在射线$AB$,$AC$上.

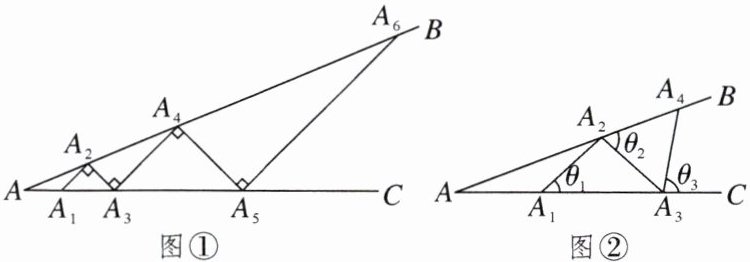
活动一:如图①所示,从点$A_1$开始,依次向右摆放小棒,使小棒在端点处互相垂直,$A_1A_2$为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答:____.(填“能”或“不能”)
(2)设$AA_1 = A_1A_2 = A_2A_3$,$\theta =$____$^{\circ}$.
活动二:如图②所示,从点$A_1$开始,用等长的小棒依次向右摆放,其中$A_1A_2$为第1根小棒,且$A_1A_2 = AA_1$.
数学思考:
(3)若已经摆放了3根小棒,则$\theta_3 = $____.(用含$\theta$的式子表示)
(4)若只能摆放4根小棒,则$\theta$的取值范围是____.

答案： 9.
(1)能　
(2)22.5　
(3)40　
(4)18°≤θ＜22.5°