《2025年时习之暑假衔接八年级数学北师大版》

1. 对角线相等且互相平分的四边形一定是()
A. 梯形
B. 矩形
C. 菱形
D. 平行四边形

答案： B

2. 四边形$ABCD的对角线相交于点O$.在下列条件中,不能判定它是矩形的是()
A. $AB= CD$,$AB// CD$,$\angle BAD= 90^{\circ}$
B. $AO= CO$,$BO= DO$,$AC= BD$
C. $\angle BAD= \angle ABC= 90^{\circ}$,$\angle BCD+\angle ADC= 180^{\circ}$
D. $\angle BAD= \angle BCD$,$\angle ABC= \angle ADC= 90^{\circ}$

答案： C

3. 在四边形$ABCD$中,若$\angle A= \angle B= \angle C= \angle D$,则四边形$ABCD$是______形.

答案： 矩

4. 如图,已知$\square ABCD$,下列条件：①$AC= BD$,②$AB= AD$,③$\angle 1= \angle 2$,④$AB\perp BC$中,其中能说明$\square ABCD$是矩形的有______(填序号).

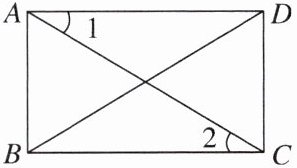
答案： ①④

5. 如图,$AC$,$BD是矩形ABCD$的两条对角线,$AE= CG= BF= DH$.求证：四边形$EFGH$是矩形.

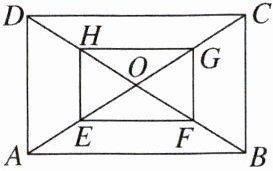
答案：
∵四边形 ABCD 为矩形，
∴AO=BO=CO=DO。又
∵AE=CG=BF=DH，
∴AO−AE=BO−BF=CO−CG=DO−DH，即 EO=FO=OG=OH。由 EO=OG，OH=OF，可知四边形 EFGH 为平行四边形。又 EO+OG=HO+FO，即 EG=HF，
∴平行四边形 EFGH 为矩形。

6. 学习了四边形的知识后,某数学兴趣小组开展检测学校雕塑(如图)底座正面四边形$ABCD$是不是一个矩形的实践活动.
[实践发现]数学兴趣小组实地勘查发现：雕塑底座正面四边形$ABCD$是一个平行四边形,但究竟是不是矩形有待验证.
[实践探究]设计测量方案：
第一步：先利用卷尺测量四条边$AD$,$BC$,$CD$,$AB$的长度,并测量出点$B$,$D$之间的距离；
第二步：通过计算验证底座正面四边形$ABCD$是不是一个矩形.
[问题解决]
(1)小明同学是这样测量的：利用卷尺测量得到边$AD$的长是60厘米,边$AB$的长是80厘米,对角线$BD$的长是100厘米,则四边形$ABCD$是矩形吗？为什么？
(2)爱动脑筋的小华同学说如果卷尺是没有刻度的,他也有办法检验四边形$ABCD$是不是矩形.请写出小华的检验方法并说明理由.

答案：
(1) 是。理由如下：
∵AD 的长是 60 厘米，边 AB 的长是 80 厘米，对角线 BD 的长是 100 厘米，
∴AD²+AB²=60²+80²=100²=BD²。
∴∠A=90°。
∵四边形 ABCD 是平行四边形，
∴四边形 ABCD 是矩形。
(2) 小华的检验方法是：检测对角线 AC，BD 是不是相等即可。理由：
∵AC=BD，四边形 ABCD 是平行四边形，
∴四边形 ABCD 是矩形。