《2025年时习之暑假衔接八年级数学北师大版》

5. 如图,过等边三角形$ABC的顶点A$作射线．若$∠1= 25^{\circ }$,则$∠2$的度数为()


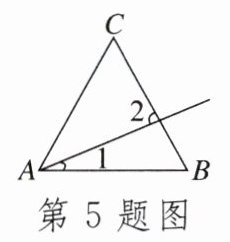
A.$85^{\circ }$
B.$45^{\circ }$
C.$105^{\circ }$
D.$125^{\circ }$

答案： A

6. 如图,已知$AD是等边三角形ABC$的高,且$BD= 1cm$,那么$BC$的长是____．

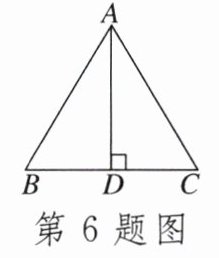
答案： 2 cm

7. 如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中$∠α+∠β$的度数是____．

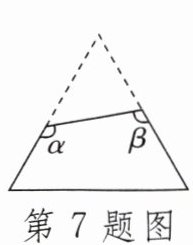
答案： 240°

8. 如图,在$\triangle ABC$中,点$D为AC$边上的一点,$DE⊥AB于点E$,$ED的延长线交BC的延长线于点F$,$CD= CF$,且$∠F= 30^{\circ }$．求证：$\triangle ABC$是等边三角形．

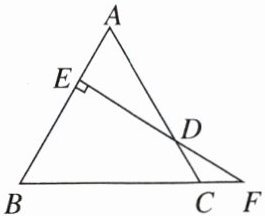
答案： $\because CD=CF,\therefore ∠CDF=∠F=30^{\circ },\therefore ∠ACB=∠F+∠CDF=60^{\circ }.$
$\because DE⊥AB,\therefore ∠A+∠ADE=90^{\circ },∠B+∠F=90^{\circ }.$
又$\because ∠CDF=∠ADE,\therefore ∠A=∠B=60^{\circ }=∠ACB,\therefore △ABC$
是等边三角形.

9. 用反证法证明“三角形中至少有一个内角不小于$60^{\circ }$”,应先假设这个三角形中()
A. 有一个内角小于$60^{\circ }$
B. 每个内角都小于$60^{\circ }$
C. 有一个内角大于$60^{\circ }$
D. 每个内角都大于$60^{\circ }$

答案： B

10. 如图,一棵树在一次强风中于离地面3米处折断倒下,倒下部分与地面的夹角为$30^{\circ }$,这棵树在折断前的高度为()

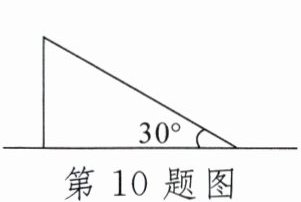
A. 6米
B. 9米
C. 12米
D. 15米

答案： B

11. 如图是某超市一层到二层滚梯示意图,其中$AB$,$CD$分别表示超市一层、二层滚梯口处地面的水平线,$∠ABC= 150^{\circ }$,$BC$的长约为12米,则乘滚梯从点$B到点C上升的高度h$约为____米．

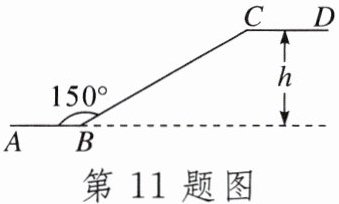
答案： 6

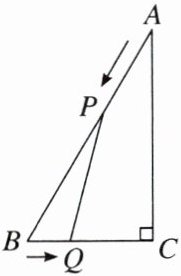
12. 如图,在$\triangle ABC$中,$∠C= 90^{\circ }$,$∠A= 30^{\circ }$,$AB= 4cm$,动点$P$,$Q同时从A$,$B$两点出发,分别在$AB$,$BC$边上匀速移动,它们的速度分别为$v_{P}= 2cm/s$,$v_{Q}= 1cm/s$,当点$P到达点B$时,$P$,$Q$两点同时停止运动．设点$P的运动时间为t\ s$．
(1)当$t$为何值时,$\triangle PBQ$为等边三角形？
(2)当$t$为何值时,$\triangle PBQ$为直角三角形？

答案： 在$△ABC$中,$∠C=90^{\circ },∠A=30^{\circ },\therefore ∠B=60^{\circ }.\because 4÷2=2,$
$\therefore 0≤t≤2$.由题可得$BP=(4-2t)cm,BQ=tcm.$
(1)当$BP=BQ$时,$△PBQ$为等边三角形,则有$4-2t=t.$
$\therefore t=\frac {4}{3}.\therefore $当$t=\frac {4}{3}$时,$△PBQ$为等边三角形.
(2)①当$∠BQP=90^{\circ }$时,$BP=2BQ$,即$4-2t=2t,\therefore t=1.$
②当$∠BPQ=90^{\circ }$时,$BQ=2BP$,即$t=2(4-2t),\therefore t=\frac {8}{5}.\therefore $当$t=$
$\frac {8}{5}$或$t=1$时,$△PBQ$为直角三角形.