2025年时习之暑假衔接八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
设计与制作风筝
风筝起源于中国,最早的风筝是由古代哲学家墨翟制造的,发明于春秋时期,至今已有2000多年的历史,北宋张择端的《清明上河图》,苏汉臣的《长春百子图》里都有放风筝的生动景象,“儿童散学归来早,忙趁东风放纸鸢”。
风筝制作在中国具有悠久的历史,以竹篾扎成鸟禽状骨架,上糊以纸,称为“纸鸢”。请根据以下任务开展制作风筝的实施过程。
任务一:了解风筝
同学们查询资料后了解到,风筝的外观形状多种多样,各具特色。下列是几种常见的风筝,其中不是轴对称图形的是______。

任务二:设计风筝
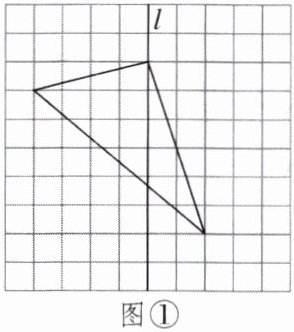
风筝由骨架、风筝面、尾巴、提线、放飞线五部分构成,如图①是同学们设计的风筝骨架的一部分。请你在图①的网格中以直线l为对称轴,画出风筝骨架的另一半。
任务三:制作风筝
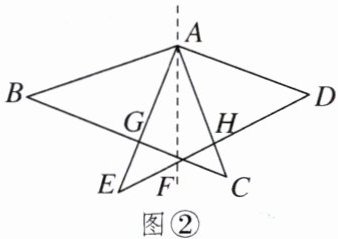
如图②所示的风筝骨架关于AF对称,已知BC= 80cm,GF= 15cm,AG= 40cm,AG⊥BC,若风筝的正反两面均为绢布,求所需绢布的面积。
任务四:活动小结
为了编写“简易风筝制作方法”,需对制作过程进行小结。请你写出一条制作过程中用到的数学知识:______。
风筝起源于中国,最早的风筝是由古代哲学家墨翟制造的,发明于春秋时期,至今已有2000多年的历史,北宋张择端的《清明上河图》,苏汉臣的《长春百子图》里都有放风筝的生动景象,“儿童散学归来早,忙趁东风放纸鸢”。
风筝制作在中国具有悠久的历史,以竹篾扎成鸟禽状骨架,上糊以纸,称为“纸鸢”。请根据以下任务开展制作风筝的实施过程。
任务一:了解风筝
同学们查询资料后了解到,风筝的外观形状多种多样,各具特色。下列是几种常见的风筝,其中不是轴对称图形的是______。

任务二:设计风筝
风筝由骨架、风筝面、尾巴、提线、放飞线五部分构成,如图①是同学们设计的风筝骨架的一部分。请你在图①的网格中以直线l为对称轴,画出风筝骨架的另一半。

任务三:制作风筝
如图②所示的风筝骨架关于AF对称,已知BC= 80cm,GF= 15cm,AG= 40cm,AG⊥BC,若风筝的正反两面均为绢布,求所需绢布的面积。

任务四:活动小结
为了编写“简易风筝制作方法”,需对制作过程进行小结。请你写出一条制作过程中用到的数学知识:______。
答案:
任务一:C
任务二:如图所示.

任务三:$\because BC=80cm,GF=15cm,AG=40cm,AG⊥BC,$$\therefore S_{\triangle ABC}=\frac {1}{2}×80×40=1600(cm^{2}),S_{\triangle AGF}=\frac {1}{2}×40×15=300(cm^{2})$.由对称的性质得$S_{\triangle ABC}=S_{\triangle ADE}=1600cm^{2},S_{\triangle AGF}=S_{\triangle AHF}=300cm^{2},\therefore S_{风筝}=1600×2 - 300×2=2600(cm^{2}).\because$ 风筝的正反两面均为绢布,
∴所需绢布的面积为$2600×2=5200(cm^{2})$.
任务四:对应点的连线被对称轴垂直平分
任务一:C
任务二:如图所示.

任务三:$\because BC=80cm,GF=15cm,AG=40cm,AG⊥BC,$$\therefore S_{\triangle ABC}=\frac {1}{2}×80×40=1600(cm^{2}),S_{\triangle AGF}=\frac {1}{2}×40×15=300(cm^{2})$.由对称的性质得$S_{\triangle ABC}=S_{\triangle ADE}=1600cm^{2},S_{\triangle AGF}=S_{\triangle AHF}=300cm^{2},\therefore S_{风筝}=1600×2 - 300×2=2600(cm^{2}).\because$ 风筝的正反两面均为绢布,
∴所需绢布的面积为$2600×2=5200(cm^{2})$.
任务四:对应点的连线被对称轴垂直平分
查看更多完整答案,请扫码查看


