2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第67页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
某中学依山而建,校门A处有一坡角$\alpha =30^{\circ }$的斜坡AB,长度为30米,在坡顶B处测得教学楼CF的楼顶C的仰角$\angle CBF= 45^{\circ }$,离B点4米远的E处有一个花台,在E处测得C的仰角$\angle CEF= 60^{\circ }$,CF的延长线交水平线AM于点D,求DC的长(结果保留根号).
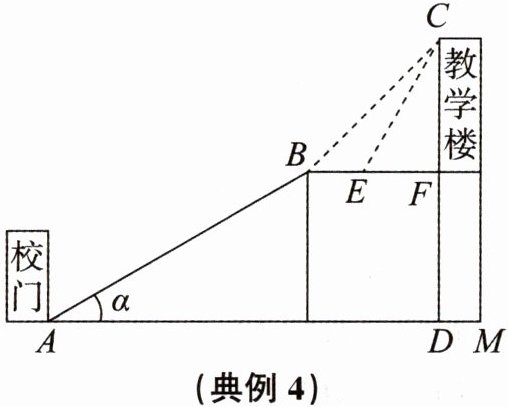

$(21 + 2\sqrt{3})$米
答案:
1. 设$CF = x$米:
因为$\angle CBF = 45^{\circ}$,$\angle BFC = 90^{\circ}$,根据$\tan\angle CBF=\frac{CF}{BF}$,$\tan45^{\circ}=1$,所以$BF = CF=x$米。
又因为$\angle CEF = 60^{\circ}$,$\angle CFE = 90^{\circ}$,根据$\tan\angle CEF=\frac{CF}{EF}$,$\tan60^{\circ}=\sqrt{3}$,则$EF=\frac{CF}{\tan60^{\circ}}=\frac{x}{\sqrt{3}}$米。
已知$BE = 4$米,且$BF - EF=BE$,所以$x-\frac{x}{\sqrt{3}} = 4$。
2. 解方程$x-\frac{x}{\sqrt{3}} = 4$:
对$x-\frac{x}{\sqrt{3}} = 4$进行变形,提取公因式$x$得$x(1 - \frac{1}{\sqrt{3}})=4$,即$x(\frac{\sqrt{3}-1}{\sqrt{3}})=4$。
则$x=\frac{4\sqrt{3}}{\sqrt{3}-1}$。
分母有理化,分子分母同乘$\sqrt{3}+1$,$x=\frac{4\sqrt{3}(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}$。
根据平方差公式$(a - b)(a + b)=a^{2}-b^{2}$,这里$a=\sqrt{3}$,$b = 1$,$(\sqrt{3}-1)(\sqrt{3}+1)=(\sqrt{3})^{2}-1^{2}=3 - 1 = 2$。
所以$x=\frac{4\sqrt{3}(\sqrt{3}+1)}{2}=2\sqrt{3}(\sqrt{3}+1)=(6 + 2\sqrt{3})$米。
在$Rt\triangle ABD$中,$\angle BAD = 30^{\circ}$,$AB = 30$米,根据$\sin\angle BAD=\frac{BD}{AB}$,$\sin30^{\circ}=\frac{1}{2}$,可得$BD=\frac{1}{2}AB = 15$米。
3. 求$DC$的长:
因为$DC=CF + FD$,而$FD = BD$。
所以$DC=x + 15$,把$x=(6 + 2\sqrt{3})$代入得$DC=(21 + 2\sqrt{3})$米。
综上,$DC$的长为$(21 + 2\sqrt{3})$米。
因为$\angle CBF = 45^{\circ}$,$\angle BFC = 90^{\circ}$,根据$\tan\angle CBF=\frac{CF}{BF}$,$\tan45^{\circ}=1$,所以$BF = CF=x$米。
又因为$\angle CEF = 60^{\circ}$,$\angle CFE = 90^{\circ}$,根据$\tan\angle CEF=\frac{CF}{EF}$,$\tan60^{\circ}=\sqrt{3}$,则$EF=\frac{CF}{\tan60^{\circ}}=\frac{x}{\sqrt{3}}$米。
已知$BE = 4$米,且$BF - EF=BE$,所以$x-\frac{x}{\sqrt{3}} = 4$。
2. 解方程$x-\frac{x}{\sqrt{3}} = 4$:
对$x-\frac{x}{\sqrt{3}} = 4$进行变形,提取公因式$x$得$x(1 - \frac{1}{\sqrt{3}})=4$,即$x(\frac{\sqrt{3}-1}{\sqrt{3}})=4$。
则$x=\frac{4\sqrt{3}}{\sqrt{3}-1}$。
分母有理化,分子分母同乘$\sqrt{3}+1$,$x=\frac{4\sqrt{3}(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}$。
根据平方差公式$(a - b)(a + b)=a^{2}-b^{2}$,这里$a=\sqrt{3}$,$b = 1$,$(\sqrt{3}-1)(\sqrt{3}+1)=(\sqrt{3})^{2}-1^{2}=3 - 1 = 2$。
所以$x=\frac{4\sqrt{3}(\sqrt{3}+1)}{2}=2\sqrt{3}(\sqrt{3}+1)=(6 + 2\sqrt{3})$米。
在$Rt\triangle ABD$中,$\angle BAD = 30^{\circ}$,$AB = 30$米,根据$\sin\angle BAD=\frac{BD}{AB}$,$\sin30^{\circ}=\frac{1}{2}$,可得$BD=\frac{1}{2}AB = 15$米。
3. 求$DC$的长:
因为$DC=CF + FD$,而$FD = BD$。
所以$DC=x + 15$,把$x=(6 + 2\sqrt{3})$代入得$DC=(21 + 2\sqrt{3})$米。
综上,$DC$的长为$(21 + 2\sqrt{3})$米。
互动题4-1 如图,小明带妹妹玩秋千,当秋千OA停止不动时,踏板与地面的距离$AB= 0.3$米.小明推了一把,秋千OA旋转到OC位置,踏板与地面的距离$CD= 1.1$米.已知$\tan \angle AOC= 0.75$,则秋千顶O与地面的距离OB为______
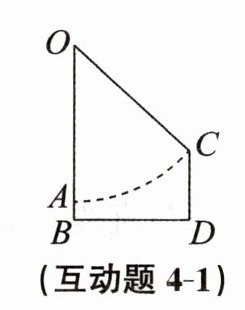
4.3
米.
答案:
4.3
互动题4-2 某区域平面示意图如图所示,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东$45^{\circ }$方向,乙勘测员在B处测得点O位于南偏西$73.7^{\circ }$方向,测得$AC= 840m$,$BC= 500m$,则点O到BC的距离约为
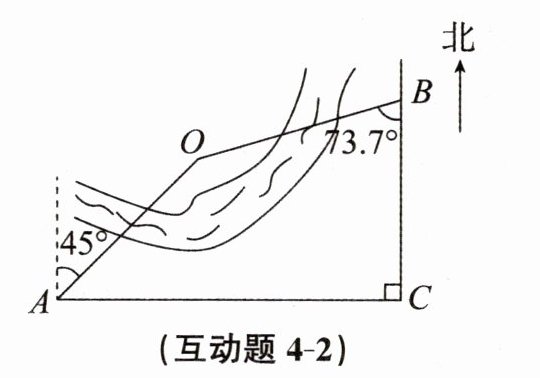
480
m(参考数据:$\sin 73.7^{\circ }\approx \frac {24}{25}$,$\cos 73.7^{\circ }\approx \frac {7}{25}$,$\tan 73.7^{\circ }\approx \frac {24}{7}$).
答案:
480
1. 如图,在边长相同的小正方形组成的网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则$\cos \angle APD$的值是(
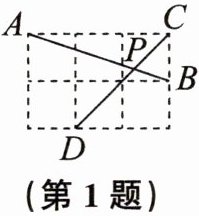
A. 0.5
B. $\frac {\sqrt {5}}{5}$
C. 2
D. $\frac {2\sqrt {5}}{5}$
B
)
A. 0.5
B. $\frac {\sqrt {5}}{5}$
C. 2
D. $\frac {2\sqrt {5}}{5}$
答案:
B
2. 在$\triangle ABC$中,若$AB= 5$,$BC= 13$,AD是BC边上的高,$AD= 4$,则$\tan C$的值是
$\frac{2}{5}$或$\frac{1}{4}$
.
答案:
$\frac{2}{5}$或$\frac{1}{4}$
3. 已知$x= \cos \alpha$($\alpha$为锐角)满足方程$2x^{2}-5x+2= 0$,求$\cos \alpha$的值.
$\frac{1}{2}$
答案:
解:对于方程$2x^{2}-5x + 2 = 0$,
因式分解得$(2x - 1)(x - 2)=0$,
则$2x - 1 = 0$或$x - 2 = 0$,
解得$x_1=\frac{1}{2}$,$x_2 = 2$。
因为$\alpha$为锐角,所以$0\lt\cos\alpha\lt1$,
而$\cos\alpha=x$,所以$\cos\alpha=\frac{1}{2}$。
因式分解得$(2x - 1)(x - 2)=0$,
则$2x - 1 = 0$或$x - 2 = 0$,
解得$x_1=\frac{1}{2}$,$x_2 = 2$。
因为$\alpha$为锐角,所以$0\lt\cos\alpha\lt1$,
而$\cos\alpha=x$,所以$\cos\alpha=\frac{1}{2}$。
4. 大连森林动物园坐落于大连市南部海滨白云山风景区内,如图①所示为大连森林动物园内的海达索道,大连能看到海的索道.图②是从莲花山观景台到南门一段索道的示意图,点A为莲花山观景台,点B是海达索道在南门的停靠点.从山脚D处看A处的仰角为$60^{\circ }$,从A处看B处的俯角为$21^{\circ }$,点A与点D之间的距离$AD= 300m$,点B到山脚的距离$BC= 40m$.求:
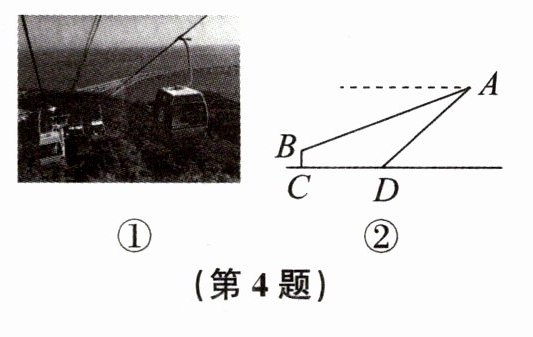
(1)点A到山脚CD的距离为
(2)AB的长为
(结果精确到1m.参考数据:$\sin 21^{\circ }\approx 0.36$,$\cos 21^{\circ }\approx 0.93$,$\tan 21^{\circ }\approx 0.38$,$\sqrt {3}\approx 1.7$)

(1)点A到山脚CD的距离为
255
m.(2)AB的长为
597
m.(结果精确到1m.参考数据:$\sin 21^{\circ }\approx 0.36$,$\cos 21^{\circ }\approx 0.93$,$\tan 21^{\circ }\approx 0.38$,$\sqrt {3}\approx 1.7$)
答案:
1. (1)
解:过点$A$作$AE\perp CD$于点$E$。
在$Rt\triangle ADE$中,$\angle ADE = 60^{\circ}$,$AD = 300m$。
根据正弦函数的定义$\sin\angle ADE=\frac{AE}{AD}$,则$AE = AD\cdot\sin\angle ADE$。
因为$\sin60^{\circ}=\frac{\sqrt{3}}{2}$,$AD = 300m$,所以$AE=300×\sin60^{\circ}=300×\frac{\sqrt{3}}{2}=150\sqrt{3}\approx150×1.7 = 255(m)$。
2. (2)
解:在$Rt\triangle ADE$中,根据余弦函数的定义$\cos\angle ADE=\frac{DE}{AD}$,则$DE = AD\cdot\cos\angle ADE$。
因为$\cos60^{\circ}=\frac{1}{2}$,$AD = 300m$,所以$DE = 300×\cos60^{\circ}=300×\frac{1}{2}=150(m)$。
已知$BC = 40m$,$AE\perp CD$,$BC\perp CD$,所以四边形$AE CB$是矩形,则$BE=AE - BC$,$AE = 255m$,$BC = 40m$,所以$BE=255 - 40=215(m)$,$EC = AB$。
又因为$EC=ED + DC$,$DC = BE$(矩形对边相等),过点$A$作$AF// CD$交$BC$的延长线于点$F$,则$\angle BAF = 21^{\circ}$,$BF=AE - BC$,$AE\perp CD$,$BC\perp CD$,$AF// CD$,所以四边形$AECF$是矩形,$BF = 215m$。
在$Rt\triangle ABF$中,$\sin\angle BAF=\frac{BF}{AB}$,则$AB=\frac{BF}{\sin\angle BAF}$。
已知$\angle BAF = 21^{\circ}$,$BF = 215m$,$\sin21^{\circ}\approx0.36$,所以$AB=\frac{215}{\sin21^{\circ}}\approx\frac{215}{0.36}\approx597(m)$。
综上,(1)点$A$到山脚$CD$的距离约为$255m$;(2)$AB$的长约为$597m$。
解:过点$A$作$AE\perp CD$于点$E$。
在$Rt\triangle ADE$中,$\angle ADE = 60^{\circ}$,$AD = 300m$。
根据正弦函数的定义$\sin\angle ADE=\frac{AE}{AD}$,则$AE = AD\cdot\sin\angle ADE$。
因为$\sin60^{\circ}=\frac{\sqrt{3}}{2}$,$AD = 300m$,所以$AE=300×\sin60^{\circ}=300×\frac{\sqrt{3}}{2}=150\sqrt{3}\approx150×1.7 = 255(m)$。
2. (2)
解:在$Rt\triangle ADE$中,根据余弦函数的定义$\cos\angle ADE=\frac{DE}{AD}$,则$DE = AD\cdot\cos\angle ADE$。
因为$\cos60^{\circ}=\frac{1}{2}$,$AD = 300m$,所以$DE = 300×\cos60^{\circ}=300×\frac{1}{2}=150(m)$。
已知$BC = 40m$,$AE\perp CD$,$BC\perp CD$,所以四边形$AE CB$是矩形,则$BE=AE - BC$,$AE = 255m$,$BC = 40m$,所以$BE=255 - 40=215(m)$,$EC = AB$。
又因为$EC=ED + DC$,$DC = BE$(矩形对边相等),过点$A$作$AF// CD$交$BC$的延长线于点$F$,则$\angle BAF = 21^{\circ}$,$BF=AE - BC$,$AE\perp CD$,$BC\perp CD$,$AF// CD$,所以四边形$AECF$是矩形,$BF = 215m$。
在$Rt\triangle ABF$中,$\sin\angle BAF=\frac{BF}{AB}$,则$AB=\frac{BF}{\sin\angle BAF}$。
已知$\angle BAF = 21^{\circ}$,$BF = 215m$,$\sin21^{\circ}\approx0.36$,所以$AB=\frac{215}{\sin21^{\circ}}\approx\frac{215}{0.36}\approx597(m)$。
综上,(1)点$A$到山脚$CD$的距离约为$255m$;(2)$AB$的长约为$597m$。
查看更多完整答案,请扫码查看


