2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第61页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 利用科学计算器求$\cos 60^{\circ}$时,依次按键$\boxed{\cos}\boxed{6}\boxed{0}\boxed{=}$,则科学计算器上显示的结果是(
A. $0.5$
B. $0.707$
C. $0.866$
D. $1$
A
)A. $0.5$
B. $0.707$
C. $0.866$
D. $1$
答案:
A
2. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 42^{\circ}$,$BC = 8$。若用科学计算器求$AC$的长,则下列按键顺序正确的是(
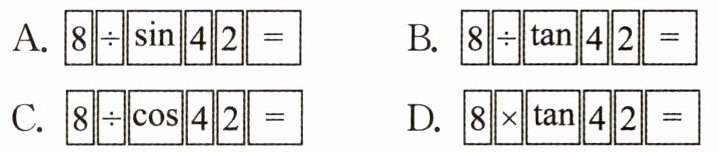
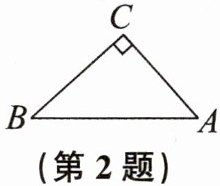
A. $\boxed{8}\boxed{÷}\boxed{\sin}\boxed{4}\boxed{2}\boxed{=}$
B. $\boxed{8}\boxed{÷}\boxed{\tan}\boxed{4}\boxed{2}\boxed{=}$
C. $\boxed{8}\boxed{÷}\boxed{\cos}\boxed{4}\boxed{2}\boxed{=}$
D. $\boxed{8}\boxed{×}\boxed{\tan}\boxed{4}\boxed{2}\boxed{=}$
D
)

A. $\boxed{8}\boxed{÷}\boxed{\sin}\boxed{4}\boxed{2}\boxed{=}$
B. $\boxed{8}\boxed{÷}\boxed{\tan}\boxed{4}\boxed{2}\boxed{=}$
C. $\boxed{8}\boxed{÷}\boxed{\cos}\boxed{4}\boxed{2}\boxed{=}$
D. $\boxed{8}\boxed{×}\boxed{\tan}\boxed{4}\boxed{2}\boxed{=}$
答案:
D
3. 有下列各式:①$\sin 20^{\circ}-\cos 20^{\circ}<0$;②$2\sin 20^{\circ}=\sin 40^{\circ}$;③$\sin 10^{\circ}+\sin 20^{\circ}=\sin 30^{\circ}$;④$\tan 20^{\circ}=\frac{\sin 20^{\circ}}{\cos 20^{\circ}}$;⑤$8\cos 30^{\circ}>\sqrt{35}$。其中正确的有(
A. ①④⑤
B. ②③④
C. ②④⑤
D. ①③④
A
)A. ①④⑤
B. ②③④
C. ②④⑤
D. ①③④
答案:
A
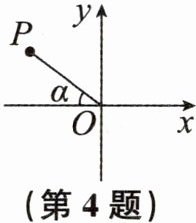
4. 在平面直角坐标系中,$O$是坐标原点,$P$是第二象限内一点,连结$OP$。若$OP与x轴负半轴之间的夹角\alpha = 37^{\circ}$,$OP = 13.5$,则点$P到x$轴的距离约为
8.10
(结果精确到$0.01$。参考数据:$\sin 37^{\circ}\approx 0.60$,$\cos 37^{\circ}\approx 0.80$,$\tan 37^{\circ}\approx 0.75$)。
答案:
8. 10
5. 用计算器求下列各式的值(结果精确到$0.0001$)。
(1)$\sin 20^{\circ}+\tan 40^{\circ}$。
(2)$\sin 44^{\circ}+2\cos 32^{\circ}15'$。
(3)$\tan 62^{\circ}17'+\frac{1}{2}\sin 89^{\circ}$。
(1)$\sin 20^{\circ}+\tan 40^{\circ}$。
(2)$\sin 44^{\circ}+2\cos 32^{\circ}15'$。
(3)$\tan 62^{\circ}17'+\frac{1}{2}\sin 89^{\circ}$。
答案:
(1)1. 181 1.
(2)2. 386 1.
(3)2. 403 3.
(1)1. 181 1.
(2)2. 386 1.
(3)2. 403 3.
6. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$。若$\tan A= \frac{2}{3}$,则$\angle A$满足(
A. $0^{\circ}<\angle A<30^{\circ}$
B. $30^{\circ}<\angle A<45^{\circ}$
C. $45^{\circ}<\angle A<60^{\circ}$
D. $60^{\circ}<\angle A<90^{\circ}$
B
)A. $0^{\circ}<\angle A<30^{\circ}$
B. $30^{\circ}<\angle A<45^{\circ}$
C. $45^{\circ}<\angle A<60^{\circ}$
D. $60^{\circ}<\angle A<90^{\circ}$
答案:
B
7. 随着科技的发展,人工智能机器人也随之进入大众的视野。如图所示为某种机器人的机械臂的一种工作状态。当两臂$AC = BC = 10m$,两臂夹角$\angle ACB = 124^{\circ}$时,求$A$,$B$两点间的距离(结果精确到$0.1m$。参考数据:$\sin 62^{\circ}\approx 0.883$,$\cos 62^{\circ}\approx 0.469$,$\tan 62^{\circ}\approx 1.881$)。
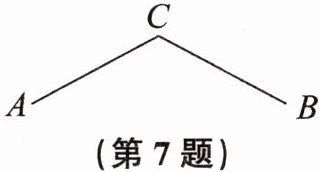

17.7 m
答案:
17. 7 m.
8. (1)如图①②,锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律(注:图①中$AB_{1}= AB_{2}= AB_{3}$)。
答:
(2)根据你探索到的规律,试分别比较$18^{\circ}$,$34^{\circ}$,$50^{\circ}$,$62^{\circ}$,$88^{\circ}$这些锐角的正弦值的大小和余弦值的大小。
正弦值:
答:
锐角的正弦值随锐角度数的增大而增大,余弦值随锐角度数的增大而减小
(2)根据你探索到的规律,试分别比较$18^{\circ}$,$34^{\circ}$,$50^{\circ}$,$62^{\circ}$,$88^{\circ}$这些锐角的正弦值的大小和余弦值的大小。
正弦值:
$\sin 18^{\circ}<\sin 34^{\circ}<\sin 50^{\circ}<\sin 62^{\circ}<\sin 88^{\circ}$
;余弦值:$\cos 18^{\circ}>\cos 34^{\circ}>\cos 50^{\circ}>\cos 62^{\circ}>\cos 88^{\circ}$
答案:
(1)锐角的正弦值随锐角度数的增大而增大,余弦值随锐角度数的增大而减小.
(2)$\sin 18^{\circ}<\sin 34^{\circ}<\sin 50^{\circ}<\sin 62^{\circ}<\sin 88^{\circ}$;$\cos 18^{\circ}>\cos 34^{\circ}>\cos 50^{\circ}>\cos 62^{\circ}>\cos 88^{\circ}$.
(1)锐角的正弦值随锐角度数的增大而增大,余弦值随锐角度数的增大而减小.
(2)$\sin 18^{\circ}<\sin 34^{\circ}<\sin 50^{\circ}<\sin 62^{\circ}<\sin 88^{\circ}$;$\cos 18^{\circ}>\cos 34^{\circ}>\cos 50^{\circ}>\cos 62^{\circ}>\cos 88^{\circ}$.
查看更多完整答案,请扫码查看


