2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第22页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
例1 现有四张正面分别标有数字$-1,0,1,2$的不透明卡片,它们除数字外其他完全相同,将它们背面朝上洗匀。若从中随机抽取一张卡片且不放回,再随机抽取一张并记下数字,前后两次抽取的数字分别记为$m,n$,请用列表或画树状图的方法,求点$(m,n)$在第一象限的概率。
答案:
$\frac{1}{6}$。
跟踪训练1-1 从$-2,-1,0,1,2$这五个数中任取一个数,作为关于$x的一元二次方程x^{2}-x+k= 0中的k$值,则所得的方程中有两个不相等的实数根的概率是
$\frac{3}{5}$
。
答案:
$\frac{3}{5}$
跟踪训练1-2 从$1,2,3,4$这4个数中任取一个数作分子,从$2,3,4$这3个数中任取一个数作分母,组成一个分数,则出现分子、分母互质的分数的概率是
$\frac{7}{12}$
。
答案:
$\frac{7}{12}$
跟踪训练1-3 形状、质地、大小、颜色完全相同的3张卡片上分别标有数字$-3,1,2$。将它们洗匀后,背面朝上,从中随机抽取1张,把抽得的数字记做$a$,再从剩下的卡片中随机抽取1张,把抽得的数字记做$b$,则使得反比例函数$y= \frac{a+b}{x}$的图象经过第一、三象限的概率是
$\frac{1}{3}$
。
答案:
$\frac{1}{3}$
例2 向如图所示的大正三角形区域内投针(区域中每个小正三角形除颜色外完全相同),针随机落在某个小正三角形内(边线忽略不计)。
(1)投针一次,针落在图中阴影区域的概率是
(2)要使针落在图中阴影区域和空白区域的概率均是$\frac{1}{2}$,还要涂黑几个小正三角形?
(1)投针一次,针落在图中阴影区域的概率是
$\frac{3}{8}$
。(2)要使针落在图中阴影区域和空白区域的概率均是$\frac{1}{2}$,还要涂黑几个小正三角形?
2 个
答案:
(1)$\frac{3}{8}$
(2)2 个。
(1)$\frac{3}{8}$
(2)2 个。
跟踪训练2-1 如图①,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为$5m$、宽为$4m$的长方形,将不规则图案围起来,然后在适当位置随机向长方形区域扔小球,并记录小球落在不规则图案内的次数(小球扔在边界线上或长方形区域外不计人试验结果),他将若干次有效试验的结果绘制成了如图②所示的折线统计图,由此可估计不规则图案的面积是(
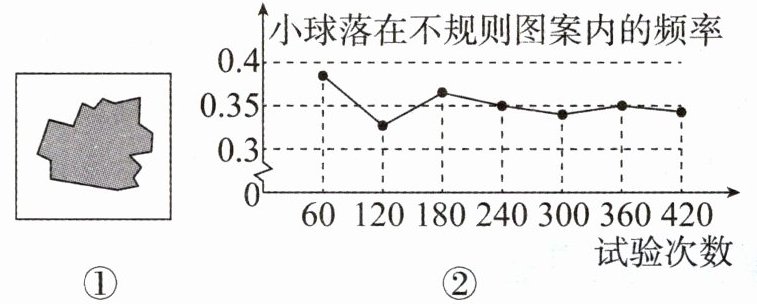
A. $6m^{2}$
B. $7m^{2}$
C. $8m^{2}$
D. $10m^{2}$
B
)
A. $6m^{2}$
B. $7m^{2}$
C. $8m^{2}$
D. $10m^{2}$
答案:
B
小镇和小海玩掷飞镖的游戏,他们设计了如图所示的矩形靶子$ABCD$,$E,F分别是边AB,CD$上的点,$EF// BC$。若小镇投中靶子,则他投掷的飞镖落在阴影部分的概率是(
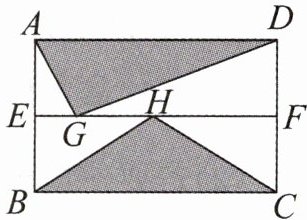
A. $\frac{1}{4}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{3}{4}$
C
)
A. $\frac{1}{4}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{3}{4}$
答案:
C
查看更多完整答案,请扫码查看


