《2025年奔跑吧少年九年级数学全一册浙教版》

11. 已知函数 $ y = \left\{ \begin{array} { l } { x ^ { 2 } + 2 ( x \leq 2 ) , } \\ { 2 x ( x ＞ 2 ) , } \end{array} \right. $ 则当函数值 $ y = 8 $ 时,自变量 $ x $ 的值是(D)
A. $ \pm \sqrt { 6 } $
B. 4
C. $ \pm \sqrt { 6 } $ 或 4
D. $ - \sqrt { 6 } $ 或 4

答案： D

12. 某型号汽车的刹车距离 $ s ( \mathrm { m } ) $ 关于速度 $ v ( \mathrm { km } / \mathrm { h } ) $ 的函数表达式为 $ s = \frac { 1 } { 100 } v ^ { 2 } $．一辆该型号汽车正以 $ 120 \mathrm { km } / \mathrm { h } $ 的速度行驶,若此时发现在前方 $ 120 \mathrm { m } $ 处停放着一辆故障车,此时刹车会(填“会”或“不会”)有危险．

答案： 会

13. 如图所示为一个迷宫游戏盘的局部平面简化示意图,该矩形的长、宽分别为

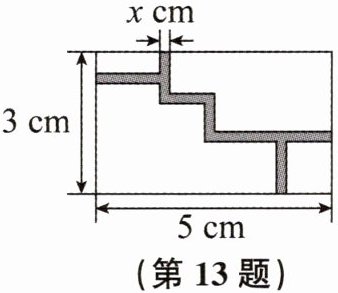
$ 5 \mathrm { cm } $,$ 3 \mathrm { cm } $,其中阴影部分为迷宫中的挡板．设挡板的宽度为 $ x ( \mathrm { cm } ) $,小球滚动的区域(空白区域)的面积为 $ y ( \mathrm { cm } ^ { 2 } ) $,则 $ y $ 关于 $ x $ 的函数表达式为$y=x^{2}-8x+15$(化简为 $ y = a x ^ { 2 } + b x + c $ 的形式)．

答案： $y=x^{2}-8x+15$

14. 已知函数 $ y = ( m ^ { 2 } + m ) x ^ { m ^ { 2 } - 2 m + 2 } + 2 x - 1 $($ m $ 为常数)．
(1)若这个函数是关于 $ x $ 的二次函数,求 $ m $ 的值．
(2)若这个函数是关于 $ x $ 的一次函数,求 $ m $ 的值．

答案：
(1)2.
(2)1 或 0 或$-1$.

15. 已知二次函数 $ y = a x ^ { 2 } + b x + c $．当 $ x = 1 $ 时,$ y = 0 $；当 $ x = 0 $ 时,$ y = - 3 $；当 $ x = - 1 $ 时,$ y = - 4 $．求这个二次函数的表达式．$y=x^{2}+2x-3$

答案： $y=x^{2}+2x-3$.

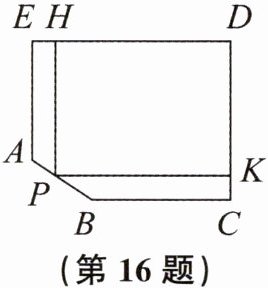
16. 如图,为了绿化小区,某物业公司要在五边形 $ A B C D E $ 的草坪上建一个矩形花坛 $ P K D H $(点 $ P $ 在 $ A B $ 上,且不与点 $ A $,$ B $ 重合)．已知 $ P H // A E $,$ P K // B C $,$ D E = 100 \mathrm { m } $,$ E A = 60 \mathrm { m } $,$ B C = 70 \mathrm { m } $,$ C D = 80 \mathrm { m } $．若 $ E H = a ( \mathrm { m } ) $,矩形 $ P K D H $ 的面积为 $ S ( \mathrm { m } ^ { 2 } ) $,求 $ S $ 关于 $ a $ 的函数表达式,并写出 $ a $ 的取值范围．

$S=$$(100-a)(60+\frac{2}{3}a)$$(0\lt a\lt30)$．

答案： $S=(100-a)(60+\frac{2}{3}a)(0\lt a\lt30)$.