2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第11页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
8. 某商店购进一批进价为每件20元的日用商品,如果以单价30元销售,那么半月内可以售出400件,根据销售经验,提高销售单价会导致销售量的减少,销售单价每提高1元,半月内的销售量相应减少20件.若设每件商品涨x元,销售利润为y元,可列函数为$y= (30+x-20)(400-20x)$.对所列函数中出现的代数式,下列说法中,错误的是(
A. $(30+x-20)$表示涨价后商品的单价
B. $20x$表示涨价后少售出商品的数量
C. $(400-20x)$表示涨价后售出商品的数量
D. $(30+x)$表示涨价后商品的单价
A
)A. $(30+x-20)$表示涨价后商品的单价
B. $20x$表示涨价后少售出商品的数量
C. $(400-20x)$表示涨价后售出商品的数量
D. $(30+x)$表示涨价后商品的单价
答案:
A
9. 如图,小明、小红两人分别从相距5km的A,C两地同时跑步出发,各自沿箭头所指方向前进.已知小明的速度是8km/h,小红的速度是6km/h,且当小明到达C地时两人停止运动,且$AC⊥CD$.出发
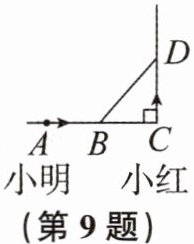
$\frac{2}{5}$
h后两人相距最近,最近距离为3
km.
答案:
$\frac{2}{5}$ 3
10. 某商铺销售一批成本为每件50元的商品,规定销售单价不低于成本价,又不高于每件70元,销售量y(件)与销售单价x(元)的关系可以近似地看做一次函数(如图).
(1)请直接写出y关于x的函数表达式:
(2)设该商铺销售这批商品获得的总利润(总利润= 总销售额-总成本)为w元,当销售单价为多少元时,可获得的总利润最大?总利润最大是多少?
当销售单价为
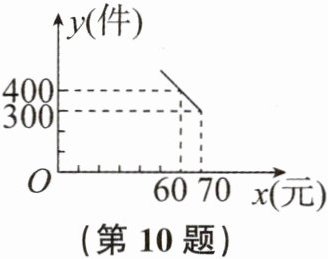
(1)请直接写出y关于x的函数表达式:
$y=-10x+1000(50\leqslant x\leqslant 70)$
.(2)设该商铺销售这批商品获得的总利润(总利润= 总销售额-总成本)为w元,当销售单价为多少元时,可获得的总利润最大?总利润最大是多少?
当销售单价为
70
元时,可获得的总利润最大,总利润最大是6000
元。
答案:
(1)$y=-10x+1000(50\leqslant x\leqslant 70)$
(2)当销售单价为70元时,可获得的总利润最大,总利润最大是6000元。
(1)$y=-10x+1000(50\leqslant x\leqslant 70)$
(2)当销售单价为70元时,可获得的总利润最大,总利润最大是6000元。
11. 一次足球训练中,小华从球门正前方11m的A处射门,足球射向球门的运行路线呈抛物线形.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门的高$OB= 2.44m$,现以O为原点建立如图所示的平面直角坐标系.
(1)请直接写出抛物线的函数表达式,并说明此次射门在不受干扰的情况下能否进球.抛物线的函数表达式为
(2)若防守队员小明正在抛物线对称轴的左侧加强防守,他的最大起跳高度是2.25m,则小明需要站在离球门多远的范围才可能防守住这次射门?小明需要站在离球门
(3)在射门路线的形状、最大高度均保持不变的情况下,适当靠近球门进球的把握会更大,小华决定将足球向球门方向移动一定距离后再射门,他最多可以向球门移动
①2.3m ②2.4m ③2.5m
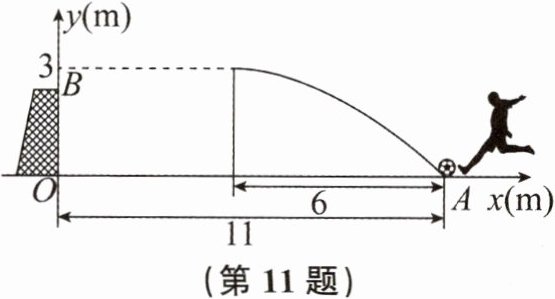
(1)请直接写出抛物线的函数表达式,并说明此次射门在不受干扰的情况下能否进球.抛物线的函数表达式为
$y=-\frac{1}{12}(x-5)^2+3$
,此次射门在不受干扰的情况下能
进球.(2)若防守队员小明正在抛物线对称轴的左侧加强防守,他的最大起跳高度是2.25m,则小明需要站在离球门多远的范围才可能防守住这次射门?小明需要站在离球门
0m~2m
的范围才可能防守住这次射门.(3)在射门路线的形状、最大高度均保持不变的情况下,适当靠近球门进球的把握会更大,小华决定将足球向球门方向移动一定距离后再射门,他最多可以向球门移动
②
(填序号,参考数据:$\sqrt {6.72}\approx 2.592$).①2.3m ②2.4m ③2.5m

答案:
(1)抛物线的函数表达式为$y=-\frac{1}{12}(x-5)^2+3$,此次射门在不受干扰的情况下能进球。
(2)小明需要站在离球门0m~2m的范围才可能防守住这次射门。
(3)②
(1)抛物线的函数表达式为$y=-\frac{1}{12}(x-5)^2+3$,此次射门在不受干扰的情况下能进球。
(2)小明需要站在离球门0m~2m的范围才可能防守住这次射门。
(3)②
查看更多完整答案,请扫码查看


