2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. (2024·杭州西湖模拟)在平面直角坐标系中,已知一次函数$y= ax+b(a≠0,$a,b是常数)的图象经过点$P(-2,0)$,且与 y 轴的正半轴相交,则二次函数$y= $$ax^{2}+bx+1$的图象可能是 (
A
)
答案:
A
2. (2024·绍兴模拟)开口向下的抛物线$y= ax^{2}+bx+1经过点(2,0)$,则下列关系式中,可能成立的是 (
A.$4a+b= 0$
B.$3a+b= 0$
C.$2a+b= 0$
D.$a+b= 0$
D
)A.$4a+b= 0$
B.$3a+b= 0$
C.$2a+b= 0$
D.$a+b= 0$
答案:
D
3. (2023·杭州西湖校级模拟改编)已知抛物线$y= x^{2}-2经过平移后得到抛物线y= x^{2}-4$,若平移前抛物线上一点的坐标是$(m,n)$,则平移后对应点的坐标是
$(m,n - 2)$
.
答案:
$(m,n - 2)$
4. (2024 秋·衢州江山期末改编)二次函数$y= ax^{2}+bx+c$(a,b,c为常数,$a≠0)$的自变量x与y的部分对应值如下表:
若$n<-1$,则点$A(bc,-a)$在第

若$n<-1$,则点$A(bc,-a)$在第
三
象限.
答案:
三
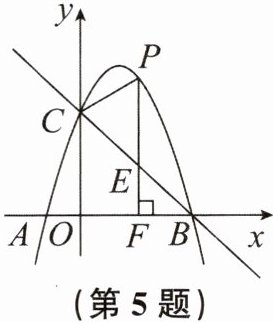
5. (2024 秋·绍兴嵊州期末)如图,抛物线$y= ax^{2}+bx+3$与x轴的交点为$A(-1,0),B(3,0)$,与y轴的交点为C.P是抛物线第一象限上一点,过点P作x轴的垂线,交x轴于点F,交直线BC于点E.
(1)求抛物线的函数表达式.
(2)当$PE= EF$时,求点E的坐标.
(3)连结PC,作点E关于PC的对称点$E'$,若$E'$落在y轴上,求点E的坐标.
(1)求抛物线的函数表达式.
(2)当$PE= EF$时,求点E的坐标.
(3)连结PC,作点E关于PC的对称点$E'$,若$E'$落在y轴上,求点E的坐标.

答案:
(1)$y = -x^{2} + 2x + 3$.
(2)$(1,2)$.
(3)$(3 - \sqrt{2},\sqrt{2})$.
(1)$y = -x^{2} + 2x + 3$.
(2)$(1,2)$.
(3)$(3 - \sqrt{2},\sqrt{2})$.
查看更多完整答案,请扫码查看


