《2025年奔跑吧少年九年级数学全一册浙教版》

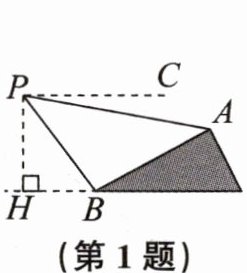
1. 如图,点P是航拍飞机在某一高度时的位置,BH是地平线,$PH⊥BH$,$PC// BH$,AB是某大型建筑物的斜面。从点P观测点B的俯角是(B)

A. $∠HPB$
B. $∠CPB$
C. $∠APB$
D. $∠PBA$

答案： B

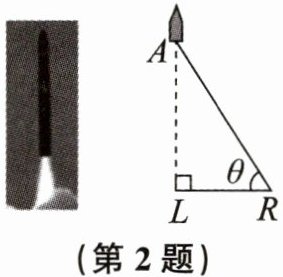
2. 2024年5月29日16时12分,“长春净月一号”卫星搭乘“谷神星一号”火箭在黄海海域成功发射。如图,当火箭上升到点A时,雷达在与发射点L相距$a(km)$的海平面R处测得其仰角为θ,则此时雷达测得火箭上升的距离AL为(A)

A. $atanθ(km)$
B. $\frac {a}{tanθ}(km)$
C. $asinθ(km)$
D. $\frac {a}{sinθ}(km)$

答案： A

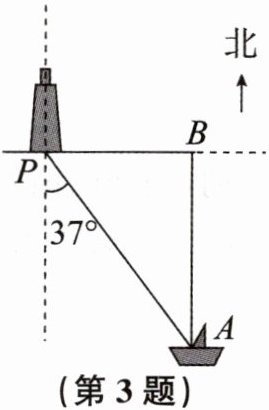
3. 如图,一艘轮船位于灯塔P的南偏东$37^{\circ }$方向,距离灯塔35海里的A处,它沿正北方向航行一段时间后,到达位于灯塔的正东方向的B处,这时,B处与灯塔P的距离PB的长可以表示为(D)

A. 35海里
B. $35cos37^{\circ }$海里
C. $35tan37^{\circ }$海里
D. $35sin37^{\circ }$海里

答案： D

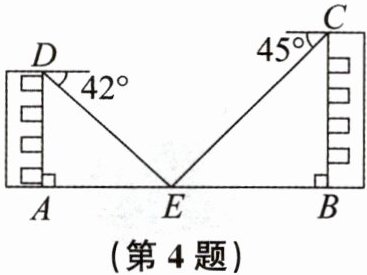
4. 如图,两幢建筑物AD和BC,$DA⊥AB$,$CB⊥AB$,$AD= 15m$,$BC= 20m$。AD和BC之间有一景观池,某同学在D点测得池中喷泉处E点的俯角为$42^{\circ }$,在C点测得E点的俯角为$45^{\circ }$,点A,E,B在同一条直线上。求得两幢建筑物之间的距离AB约为(结果精确到0.1m。参考数据：$sin42^{\circ }\approx 0.67$,$cos42^{\circ }\approx 0.74$,$tan42^{\circ }\approx 0.90$)(A)

A. 36.7m
B. 37.6m
C. 39.2m
D. 38.1m

答案： A

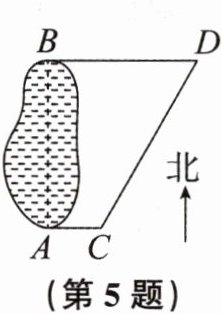
5. 如图,C,D分别表示的是一个湖泊的南、北两端A和B正东方向的两个村庄,村庄D位于村庄C的北偏东$30^{\circ }$方向上。若$CD= 8km$,则该湖泊南、北两端的距离AB为$4\sqrt{3}$km(结果保留根号)。

答案： $ 4\sqrt{3} $

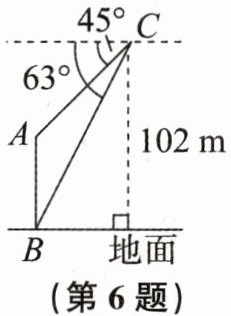
6. 某数学小组用无人机测量某建筑物AB的高度,过程如下：如图,将无人机垂直上升至距水平地面102m的C处,测得该建筑物顶端A的俯角为$45^{\circ }$,底端B的俯角为$63^{\circ }$,则测得该建筑物的高度约是51m(结果精确到1m。参考数据：$tan63^{\circ }\approx 2$,$sin63^{\circ }\approx 1$,$cos63^{\circ }\approx 0.5$)。

答案： 51

7. 如图,一款可调节的笔记本电脑支架放置在水平桌面上,通过调节BA与CB的仰角α,β的大小来达成个人舒适的高度,已知调节杆$CB= 11cm$,$AB= 20cm$,AB的最大仰角α为$53^{\circ }$。
(1)当点B离桌面的高度大约5cm时,手腕最舒适,问：应该调整哪个角的大小？调整为多少度？
应该调整β的大小，调整约为27°.
(2)在(1)的条件下,求点A到桌面的最大高度。
21 cm.
(参考数据：$sin53^{\circ }\approx 0.80$,$cos53^{\circ }\approx 0.60$,$tan53^{\circ }\approx 1.33$,$sin27^{\circ }\approx 0.45$,$cos27^{\circ }\approx 0.89$)

答案：
(1)应该调整 $ \beta $ 的大小，调整约为 $ 27^{\circ} $.
(2)21 cm.