2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第40页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
典例1 (2024秋·绍兴诸暨期末)若$\odot O内有一点P$,点$P到圆心O$的距离为5,则$\odot O的半径r$可以是(
A. 3
B. 4
C. 5
D. 6
D
)A. 3
B. 4
C. 5
D. 6
答案:
D
互动题1-1 在平面直角坐标系中,如果$\odot O是以原点O(0,0)$为圆心,10为半径的圆,那么点$A(-8,6)$(
A. 在$\odot O$内
B. 在$\odot O$外
C. 在$\odot O$上
D. 不能确定
C
)A. 在$\odot O$内
B. 在$\odot O$外
C. 在$\odot O$上
D. 不能确定
答案:
C
互动题1-2 如图,已知$\odot O和直线l$,过圆心$O作OP\perp l$,$P$为垂足,$A为直线l$上一点,且$PA= 2cm$.若$\odot O$的半径为5cm,$OP= 4cm$,则点$A在\odot O$
内
.
答案:
内
典例2 (2024秋·宁波海曙期末)已知$\odot M与x轴相交于点A(2,0)$,$B(-6,0)$,与$y轴相交于点C(0,4)$,$D(0,-3)$,则圆心$M$的坐标是
$(-2,\frac {1}{2})$
.
答案:
$(-2,\frac {1}{2})$
互动题2-1 如图,在平面直角坐标系$xOy$中,点$A(0,3)$,$B(2,1)$,$C(2,-3)$,则由画图操作可知,$\triangle ABC$的外接圆的圆心坐标是(
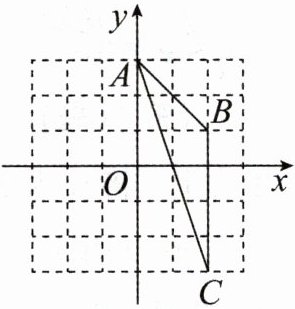
A. $(-2,-1)$
B. $(-1,0)$
C. $(-1,-1)$
D. $(0,-1)$
A
)
A. $(-2,-1)$
B. $(-1,0)$
C. $(-1,-1)$
D. $(0,-1)$
答案:
A
互动题2-2 平面上有4个点,它们不在同一直线上,过其中3个点作圆,可以作出不重复的圆$n$个,则$n$的值不可能为(
A. 4
B. 3
C. 2
D. 1
C
)A. 4
B. 3
C. 2
D. 1
答案:
C
典例3 (2024秋·湖州期末)如图,将$\triangle OAB绕点O按逆时针方向旋转90^{\circ}得到\triangle OCD$,已知$\angle AOB= 30^{\circ}$,则$\angle BOC= $______
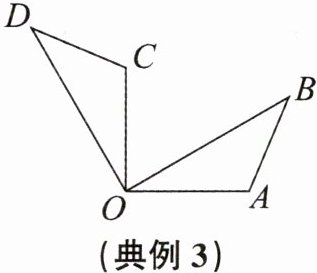
$60^{\circ }$
.
答案:
$60^{\circ }$
互动题3-1 如图,$\triangle ABC绕点A按逆时针方向旋转20^{\circ}得到\triangle AB'C'$,点$C恰好落在B'C'$上,则$\angle ACB$的度数为(
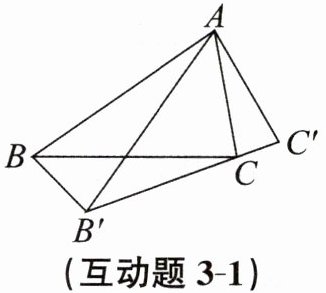
A. $60^{\circ}$
B. $70^{\circ}$
C. $80^{\circ}$
D. $90^{\circ}$
C
)
A. $60^{\circ}$
B. $70^{\circ}$
C. $80^{\circ}$
D. $90^{\circ}$
答案:
C
互动题3-2 如图,将$\triangle ABC绕点A按顺时针方向旋转90^{\circ}得到\triangle ADE$,点$B$,$C的对应点分别为点D$,$E$,连结$CE$,点$D恰好落在线段CE$上,若$CD= 6$,$BC= 2$,则$AE$的长为(
A. $4\sqrt{2}$
B. 6
C. $2\sqrt{10}$
D. 8
A
)A. $4\sqrt{2}$
B. 6
C. $2\sqrt{10}$
D. 8
答案:
A
典例4 (2024秋·绍兴越城期末)日常生活中常见的装饰盘由圆盘和支架组成(如图①),它可以看作如图②所示的几何图形.已知$AC= BD= 5cm$,$AC\perp CD$,垂足为$C$,$BD\perp CD$,垂足为$D$,$CD= 16cm$,$\odot O的半径r= 10cm$,则圆盘离桌面$CD$最近的距离是
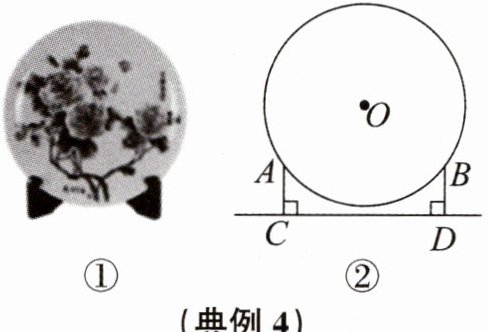
1
cm.
答案:
1
互动题4-1 如图,$\odot O$的半径为5cm,$P是\odot O$外一点,$OP= 8cm$,$\angle P= 30^{\circ}$,则$PB$的长为
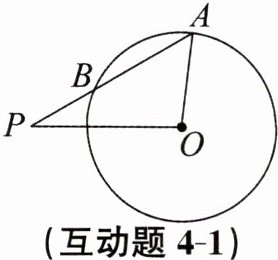
$(4\sqrt {3}-3)$
cm.
答案:
$(4\sqrt {3}-3)$
查看更多完整答案,请扫码查看


