2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第60页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,在$Rt△ABC$中,$∠C= 90^{\circ }$,$AC= 4$,$AB= 5$,则$sinB$的值为(
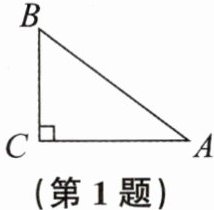
A. $\frac {2}{3}$
B. $\frac {3}{5}$
C. $\frac {3}{4}$
D. $\frac {4}{5}$
D
)
A. $\frac {2}{3}$
B. $\frac {3}{5}$
C. $\frac {3}{4}$
D. $\frac {4}{5}$
答案:
D
2. 在$Rt△ABC$中,$∠C= 90^{\circ }$,$tanA= \frac {3}{4}$,若将$△ABC$的三边都扩大3倍,则$tanA$的值为(
A. $\frac {3}{4}$
B. $\frac {4}{3}$
C. $\frac {9}{4}$
D. $\frac {12}{5}$
A
)A. $\frac {3}{4}$
B. $\frac {4}{3}$
C. $\frac {9}{4}$
D. $\frac {12}{5}$
答案:
A
3. 在$Rt△ABC$中,$∠C= 90^{\circ }$,$sinA= \frac {5}{13}$,$BC= 10$,则$AB$的长为
26
.
答案:
26
4. 如图,$△ABC$的顶点都在正方形网格的格点上,则$cos∠ACB$的值为
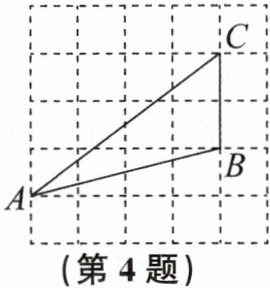
$\frac{3}{5}$
.
答案:
$\frac{3}{5}$
5. 如图,在$Rt△ABC$中,$∠C= 90^{\circ }$,$BC= 2$,$sinA= \frac {1}{3}$,求$AC=$
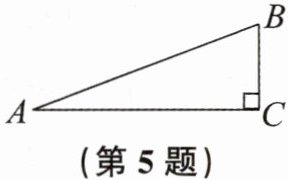
$4\sqrt{2}$
,$AB=$6
及$sinB=$$\frac{2\sqrt{2}}{3}$
的值.
答案:
1. 首先求$AB$的值:
在$Rt\triangle ABC$中,根据正弦函数的定义$\sin A=\frac{BC}{AB}$。
已知$BC = 2$,$\sin A=\frac{1}{3}$,由$\sin A=\frac{BC}{AB}$可得$AB=\frac{BC}{\sin A}$。
把$BC = 2$,$\sin A=\frac{1}{3}$代入$AB=\frac{BC}{\sin A}$,则$AB=\frac{2}{\frac{1}{3}} = 6$。
2. 然后求$AC$的值:
根据勾股定理$AC=\sqrt{AB^{2}-BC^{2}}$。
已知$AB = 6$,$BC = 2$,则$AC=\sqrt{6^{2}-2^{2}}=\sqrt{36 - 4}=\sqrt{32}=4\sqrt{2}$。
3. 最后求$\sin B$的值:
根据正弦函数的定义$\sin B=\frac{AC}{AB}$。
把$AC = 4\sqrt{2}$,$AB = 6$代入$\sin B=\frac{AC}{AB}$,则$\sin B=\frac{4\sqrt{2}}{6}=\frac{2\sqrt{2}}{3}$。
综上,$AC = 4\sqrt{2}$,$AB = 6$,$\sin B=\frac{2\sqrt{2}}{3}$。
在$Rt\triangle ABC$中,根据正弦函数的定义$\sin A=\frac{BC}{AB}$。
已知$BC = 2$,$\sin A=\frac{1}{3}$,由$\sin A=\frac{BC}{AB}$可得$AB=\frac{BC}{\sin A}$。
把$BC = 2$,$\sin A=\frac{1}{3}$代入$AB=\frac{BC}{\sin A}$,则$AB=\frac{2}{\frac{1}{3}} = 6$。
2. 然后求$AC$的值:
根据勾股定理$AC=\sqrt{AB^{2}-BC^{2}}$。
已知$AB = 6$,$BC = 2$,则$AC=\sqrt{6^{2}-2^{2}}=\sqrt{36 - 4}=\sqrt{32}=4\sqrt{2}$。
3. 最后求$\sin B$的值:
根据正弦函数的定义$\sin B=\frac{AC}{AB}$。
把$AC = 4\sqrt{2}$,$AB = 6$代入$\sin B=\frac{AC}{AB}$,则$\sin B=\frac{4\sqrt{2}}{6}=\frac{2\sqrt{2}}{3}$。
综上,$AC = 4\sqrt{2}$,$AB = 6$,$\sin B=\frac{2\sqrt{2}}{3}$。
6. 如图,已知$tanα= \frac {1}{2}$,若$F(4,y)是射线OA$上的点,则点$F$的坐标是
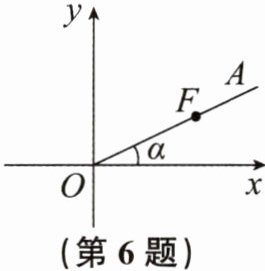
$(4,2)$
.
答案:
$(4,2)$
7. 如图,在半径为3的$\odot O$中,直径$AB与弦CD相交于点E$,连结$AC$,$BD$.若$AC= 2$,求$cosD$的值.
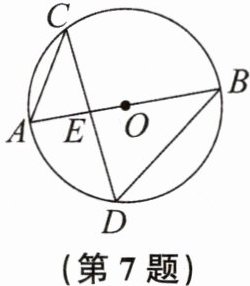
$\frac{1}{3}$

答案:
1. 首先,根据圆周角定理:
因为$\angle D$和$\angle A$所对的弧都是$\overset{\frown}{BC}$,所以$\angle D=\angle A$。
2. 然后,连接$BC$:
因为$AB$是$\odot O$的直径,所以$\angle ACB = 90^{\circ}$(直径所对的圆周角是直角)。
已知$\odot O$的半径$r = 3$,则直径$AB=2r = 6$,$AC = 2$。
3. 最后,根据余弦的定义求$\cos A$:
在$Rt\triangle ABC$中,根据余弦的定义$\cos A=\frac{AC}{AB}$(在直角三角形中,一个锐角的余弦等于邻边与斜边的比值)。
把$AC = 2$,$AB = 6$代入$\cos A=\frac{AC}{AB}$,可得$\cos A=\frac{2}{6}=\frac{1}{3}$。
因为$\angle D=\angle A$,所以$\cos D=\cos A=\frac{1}{3}$。
故$\cos D$的值为$\frac{1}{3}$。
因为$\angle D$和$\angle A$所对的弧都是$\overset{\frown}{BC}$,所以$\angle D=\angle A$。
2. 然后,连接$BC$:
因为$AB$是$\odot O$的直径,所以$\angle ACB = 90^{\circ}$(直径所对的圆周角是直角)。
已知$\odot O$的半径$r = 3$,则直径$AB=2r = 6$,$AC = 2$。
3. 最后,根据余弦的定义求$\cos A$:
在$Rt\triangle ABC$中,根据余弦的定义$\cos A=\frac{AC}{AB}$(在直角三角形中,一个锐角的余弦等于邻边与斜边的比值)。
把$AC = 2$,$AB = 6$代入$\cos A=\frac{AC}{AB}$,可得$\cos A=\frac{2}{6}=\frac{1}{3}$。
因为$\angle D=\angle A$,所以$\cos D=\cos A=\frac{1}{3}$。
故$\cos D$的值为$\frac{1}{3}$。
8. 如图,在$Rt△ABC$中,$∠C= 90^{\circ }$,$a$,$b$,$c分别表示Rt△ABC中∠A$,$∠B$,$∠C$的对边.
(1)求$sinA$,$cosB$.
$sinA$=
(2)求$tanA$,$tanB$,$tanA\cdot tanB$.
$tanA$=
(3)观察(1)(2)中的计算结果,若$α+β= 90^{\circ }$,试猜想$sinα与cosβ$,$tanα与tanβ$之间的关系.
$sinα$与$cosβ$的关系为
(4)应用:①在$Rt△ABC$中,$∠C= 90^{\circ }$,$sinA= \frac {2}{3}$,则$cosB$的值为____
②在$Rt△ABC$中,$∠C= 90^{\circ }$,$tanA= 2$,则$tanB$的值为____
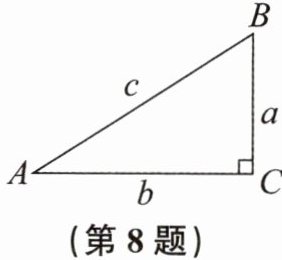
(1)求$sinA$,$cosB$.
$sinA$=
$\frac{a}{c}$
,$cosB$=$\frac{a}{c}$
.(2)求$tanA$,$tanB$,$tanA\cdot tanB$.
$tanA$=
$\frac{a}{b}$
,$tanB$=$\frac{b}{a}$
,$tanA\cdot tanB$=1
.(3)观察(1)(2)中的计算结果,若$α+β= 90^{\circ }$,试猜想$sinα与cosβ$,$tanα与tanβ$之间的关系.
$sinα$与$cosβ$的关系为
$sinα = cosβ$
,$tanα$与$tanβ$的关系为$tanα \cdot tanβ = 1$
.(4)应用:①在$Rt△ABC$中,$∠C= 90^{\circ }$,$sinA= \frac {2}{3}$,则$cosB$的值为____
$\frac{2}{3}$
.②在$Rt△ABC$中,$∠C= 90^{\circ }$,$tanA= 2$,则$tanB$的值为____
$\frac{1}{2}$
.
答案:
1. (1)
根据正弦函数和余弦函数的定义:
在$Rt\triangle ABC$中,$\sin A=\frac{a}{c}$,$\cos B = \frac{a}{c}$。
2. (2)
根据正切函数的定义:
$\tan A=\frac{a}{b}$,$\tan B=\frac{b}{a}$。
则$\tan A\cdot\tan B=\frac{a}{b}\cdot\frac{b}{a}=1$。
3. (3)
由(1)可知:若$\alpha+\beta = 90^{\circ}$,则$\sin\alpha=\cos\beta$;
由(2)可知:若$\alpha+\beta = 90^{\circ}$,则$\tan\alpha\cdot\tan\beta = 1$。
4. (4)
①
因为$\angle A+\angle B = 90^{\circ}$,根据$\sin\alpha=\cos\beta(\alpha+\beta = 90^{\circ})$,已知$\sin A=\frac{2}{3}$,所以$\cos B=\sin A=\frac{2}{3}$。
②
因为$\angle A+\angle B = 90^{\circ}$,根据$\tan\alpha\cdot\tan\beta = 1(\alpha+\beta = 90^{\circ})$,已知$\tan A = 2$,设$\tan B=x$,则$2x = 1$,解得$x=\frac{1}{2}$,所以$\tan B=\frac{1}{2}$。
综上,答案依次为:(1)$\sin A=\frac{a}{c}$,$\cos B=\frac{a}{c}$;(2)$\tan A=\frac{a}{b}$,$\tan B=\frac{b}{a}$,$\tan A\cdot\tan B = 1$;(3)$\sin\alpha=\cos\beta$,$\tan\alpha\cdot\tan\beta = 1$;(4)①$\frac{2}{3}$;②$\frac{1}{2}$。
根据正弦函数和余弦函数的定义:
在$Rt\triangle ABC$中,$\sin A=\frac{a}{c}$,$\cos B = \frac{a}{c}$。
2. (2)
根据正切函数的定义:
$\tan A=\frac{a}{b}$,$\tan B=\frac{b}{a}$。
则$\tan A\cdot\tan B=\frac{a}{b}\cdot\frac{b}{a}=1$。
3. (3)
由(1)可知:若$\alpha+\beta = 90^{\circ}$,则$\sin\alpha=\cos\beta$;
由(2)可知:若$\alpha+\beta = 90^{\circ}$,则$\tan\alpha\cdot\tan\beta = 1$。
4. (4)
①
因为$\angle A+\angle B = 90^{\circ}$,根据$\sin\alpha=\cos\beta(\alpha+\beta = 90^{\circ})$,已知$\sin A=\frac{2}{3}$,所以$\cos B=\sin A=\frac{2}{3}$。
②
因为$\angle A+\angle B = 90^{\circ}$,根据$\tan\alpha\cdot\tan\beta = 1(\alpha+\beta = 90^{\circ})$,已知$\tan A = 2$,设$\tan B=x$,则$2x = 1$,解得$x=\frac{1}{2}$,所以$\tan B=\frac{1}{2}$。
综上,答案依次为:(1)$\sin A=\frac{a}{c}$,$\cos B=\frac{a}{c}$;(2)$\tan A=\frac{a}{b}$,$\tan B=\frac{b}{a}$,$\tan A\cdot\tan B = 1$;(3)$\sin\alpha=\cos\beta$,$\tan\alpha\cdot\tan\beta = 1$;(4)①$\frac{2}{3}$;②$\frac{1}{2}$。
查看更多完整答案,请扫码查看


