《2025年奔跑吧少年九年级数学全一册浙教版》

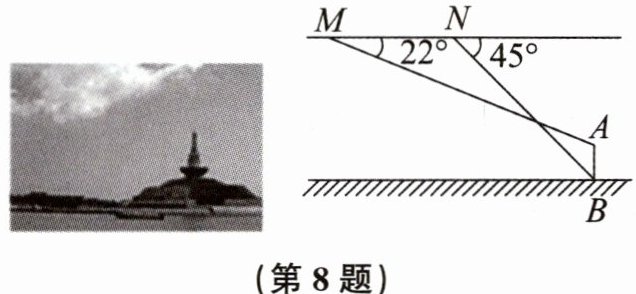
8. 某数学兴趣小组用无人机测量潮汐塔AB的高度,测量方案如图所示：无人机在距水平地面119m的点M处测得潮汐塔顶端A的俯角为$22^{\circ }$,再将无人机沿水平方向飞行74m到达点N,测得潮汐塔底端B的俯角为$45^{\circ }$(点M,N,A,B在同一平面内),则潮汐塔AB的高度约为(结果精确到1m。参考数据：$sin22^{\circ }\approx 0.37$,$cos22^{\circ }\approx 0.93$,$tan22^{\circ }\approx 0.40$)(B)

A. 41m
B. 42m
C. 48m
D. 51m

答案： B

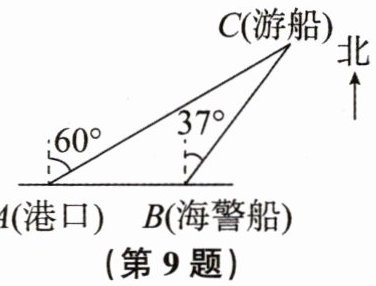
9. 一艘观光游船从港口A以北偏东$60^{\circ }$的方向出港观光,航行80海里至C处时发生了侧翻事故,立即发出了求救信号。一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东$37^{\circ }$方向,马上以40海里/时的速度前往救援。海警船大约需$\frac{5}{4}$小时到达事故船C处(参考数据：$sin53^{\circ }\approx 0.8$,$cos53^{\circ }\approx 0.6$)。

答案： $ \frac{5}{4} $

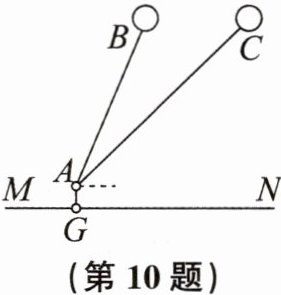
10. “儿童散学归来早,忙趁东风放纸鸢。”随着春季的来临,放风筝已成为孩子们的最爱。周末小冬和爸爸一起去公园放风筝,如图,当小冬站在G处时,风筝在空中的位置为点B,仰角为$67^{\circ }$,小冬站在G处继续放线,当再放2米长的线时,风筝飞到点C处,此时点B,C离地面MN的高度恰好相等,C点的仰角为$44^{\circ }$。若小冬的眼睛与地面MN的距离AG为1.6米,请计算风筝离地面MN的高度(结果保留整数。参考数据：$sin44^{\circ }\approx 0.7$,$sin67^{\circ }\approx 0.9$,$cos67^{\circ }\approx 0.4$)。

8 米

答案： 8 米.

11. 在“综合与实践”活动中,瑶瑶计划借助无人机测量酒店大楼AB的高度,她设计了如下测量方案：
如图,瑶瑶站在离酒店大楼水平距离为40米的广场高地E处,E处高出地面的距离$CE= 2.4$米,无人机旋停在点C正上方的点D处,测得酒店大楼AB的顶部B处的俯角α的正切值是$\frac {1}{2}$,此时无人机离地面的高度CD为120米,已知瑶瑶的目高(眼睛到地面的距离)$EF= 1.6$米。
(1)求酒店大楼AB的高度。100 米
(2)若无人机保持现有高度沿平行于CA的方向,以4米/秒的速度继续向前匀速飞行,经过12秒时,无人机是否离开瑶瑶的视线FB？请说明理由。无人机没有离开瑶瑶的视线 $ FB $，理由略

答案：
(1)100 米.
(2)无人机没有离开瑶瑶的视线 $ FB $，理由略.