2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第15页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
典例3 (2024秋·金华义乌期末)如图,二次函数$y= ax^{2}+bx+c的图象的对称轴是直线x= -1$,与x轴的一个交点为$(-5,0)$,则关于x的不等式$ax^{2}+bx+c≥0$的
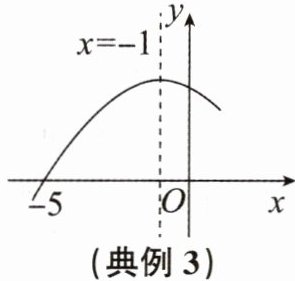
解为

解为
$-5\leqslant x\leqslant3$
.
答案:
$-5\leqslant x\leqslant3$
互动题3-1 如图,抛物线$y= ax^{2}+bx+c与直线y= mx+n相交于点A(-2,0),B(0,-2)$,则关于x的不等式$ax^{2}+bx+c<mx+n$的解为
$-2<x<0$
.
答案:
$-2<x<0$
互动题3-2 如图,二次函数$y= ax^{2}+bx+c(a≠0)$的图象过点(-2,0),(4,0),(-1,-2.5),则一元二次方程$ax^{2}+bx+c= -2.5$的根为
$x_1=-1,x_2=3$
.
答案:
$x_1=-1,x_2=3$
典例4-1 (2024秋·嘉兴期末)如图所示为一座拱桥的示意图,桥洞的拱是抛物线形,已知水面宽12m,桥洞顶部离水面4m.
(1)请在示意图中建立合适的平面直角坐标系,并求出抛物线的函数表达式.
(2)若有一艘船,宽度为4m,高度为3m,则这艘船能否从该桥下通过?
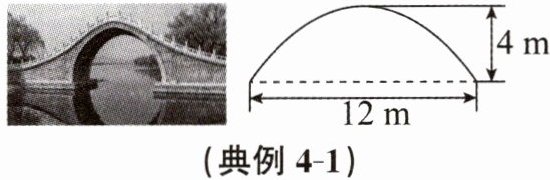
(1)请在示意图中建立合适的平面直角坐标系,并求出抛物线的函数表达式.
略
(2)若有一艘船,宽度为4m,高度为3m,则这艘船能否从该桥下通过?
能

答案:
(1)略
(2)能.
(1)略
(2)能.
互动题4-1 【问题情境】如图所示为喷水管OA从点A向四周喷出水花时的喷泉截面示意图,喷出的水花是相同的抛物线形.以O为原点,建立平面直角坐标系,以水平方向为x轴,OA所在直线为y轴,点C,D为x轴上水花的落水点,其中y轴右侧抛物线的函数表达式为$y= -\frac {1}{6}(x-4)^{2}+5(x≥0).$
【问题解决】(1)求喷水管OA的高度.
(2)现重新改建喷泉,降低喷水管,使落水点与喷水管的水平距离为9m,求喷水管OA要降低的高度.
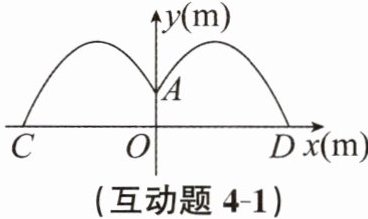
【问题解决】(1)求喷水管OA的高度.
$\frac{7}{3}$m
(2)现重新改建喷泉,降低喷水管,使落水点与喷水管的水平距离为9m,求喷水管OA要降低的高度.
$\frac{5}{6}$m

答案:
(1)$\frac{7}{3}$m.
(2)$\frac{5}{6}$m.
(1)$\frac{7}{3}$m.
(2)$\frac{5}{6}$m.
查看更多完整答案,请扫码查看


