2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第23页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 方方写了一段简单的计算机程序代码,可以在$1,2,3,4,5,6$这六个数中,随机选择一个为字母$a$的值,则程序运行后能使不等式$a>4$成立的概率是(
A. $\frac{1}{6}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{2}{3}$
B
)A. $\frac{1}{6}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{2}{3}$
答案:
B
2. 如图所示为一个游戏转盘。自由转动转盘,当转盘停止转动后,指针最大可能落在(
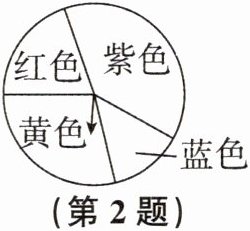
A. 紫色区域
B. 红色区域
C. 黄色区域
D. 蓝色区域
A
)
A. 紫色区域
B. 红色区域
C. 黄色区域
D. 蓝色区域
答案:
A
3. 在$-2,-1,0,1,2这五个数中任取两个作为m,n$的值,则二次函数$y= (x-m)^{2}+n$的顶点在坐标轴上的概率是(
A. $\frac{2}{5}$
B. $\frac{1}{5}$
C. $\frac{1}{4}$
D. $\frac{1}{2}$
A
)A. $\frac{2}{5}$
B. $\frac{1}{5}$
C. $\frac{1}{4}$
D. $\frac{1}{2}$
答案:
A
4. 如图所示为4张不透明的卡片,它们除正面的函数表达式不同外,其余均相同。将它们背面朝上洗匀后,从中随机抽取1张卡片,则抽到函数图象不经过第四象限的卡片的概率是______

$\frac{3}{4}$
。
答案:
$\frac{3}{4}$
5. 如图,在$3×3$正方形网格中,$A,B$在格点上,在网格的其他格点上任取一点$C$(不与点$A,B$重合),能使$\triangle ABC$为等腰三角形的概率是
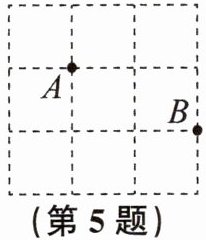
$\frac{5}{14}$
。
答案:
$\frac{5}{14}$
6. 已知函数$y= (2k-1)x+4$($k$为常数),若从$-3\leqslant k\leqslant 3中任取k$的值,则得到的函数是具有“$y随x$的增大而增大”这一性质的一次函数的概率是
$\frac{5}{12}$
。
答案:
$\frac{5}{12}$
7. 如图,将一个棱长为3的立方体的表面涂上红色,再把它分割成棱长为1的小立方体,从中任取一个小立方体,则取得的小立方体恰有三个面涂有红色的概率是
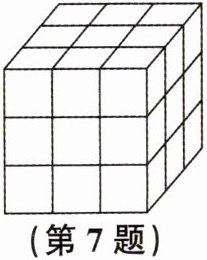
$\frac{8}{27}$
。
答案:
$\frac{8}{27}$
8. 某班有50名学生,每名学生都有一个序号。将50张编有学生序号(从1号到50号)的卡片(除序号不同外其他均相同)充分洗匀,从中任意抽取1张。
(1)求抽取到的卡片上序号是20的倍数或能整除20的概率。
(2)若抽取到的卡片上序号是$k$($k是满足1\leqslant k\leqslant 50$的整数),则规定$k的倍数或能整除k$(不重复计数)的序号的学生能参加某项活动。这一规定是否公平?请说明理由。
(1)求抽取到的卡片上序号是20的倍数或能整除20的概率。
(2)若抽取到的卡片上序号是$k$($k是满足1\leqslant k\leqslant 50$的整数),则规定$k的倍数或能整除k$(不重复计数)的序号的学生能参加某项活动。这一规定是否公平?请说明理由。
答案:
(1)$\frac{7}{50}$。
(2)不公平,理由略。
(1)$\frac{7}{50}$。
(2)不公平,理由略。
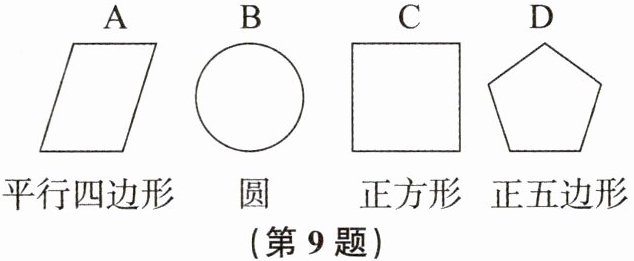
9. 有4张背面完全相同的纸牌$A,B,C,D$,其中正面分别画有如图所示4个不同的几何图形,小华将这4张纸牌背面朝上洗匀后摸出1张,放回洗匀后再摸出1张。
(1)用列表或画树状图的方法表示两次摸牌所有可能的结果(纸牌用$A,B,C,D$表示)。
(2)求摸出的两张纸牌正面所画的几何图形既是轴对称图形又是中心对称图形的概率。
(1)用列表或画树状图的方法表示两次摸牌所有可能的结果(纸牌用$A,B,C,D$表示)。
略
(2)求摸出的两张纸牌正面所画的几何图形既是轴对称图形又是中心对称图形的概率。
$\frac{1}{4}$

答案:
(1)略
(2)$\frac{1}{4}$。
(1)略
(2)$\frac{1}{4}$。
查看更多完整答案,请扫码查看


