《2025年核心素养天天练六年级数学下册北师大版》

1. 选一选。
(1)用一块长25.12cm、宽18.84cm的长方形铁皮，配上下面(　　　)圆形铁片正好可以做成圆柱形容器。

①$r = 1$ cm ②$d = 3$ cm ③$r = 4$ cm ④$d = 6$ cm
A. ①③ B. ①② C. ③④ D. ②④

答案：
(1)C 解析：根据圆柱的特征，并利用圆的周长公式：直径 = 周长÷π，用长方形铁皮的长和宽分别除以π，求出长围成的圆的直径，宽围成的圆的直径；再和圆形铁片的直径比较，相等就可以做成圆柱形容器。

(2)[北京顺义区期末]妈妈榨了一大杯橙汁招待客人，倒入小杯子中(如图)，可以倒满( )杯。

A. 3 B. 6 C. 9 D. 15

答案：
(2)C
解析：根据圆柱体积 = 底面积×高，圆锥体积 = 底面积×高÷3，分别求出橙汁体积和小杯子容积，用橙汁体积÷小杯子容积，结果即为所求。

(3)[山东菏泽郓城县期末]把一个圆柱形木块截成两部分(如图)，上、下两部分体积的比是( )。
A. 1 : 4 B. 3 : 2 C. 2 : 3 D. 1 : 1

答案：
(3)C
解析：图形的底面积相同，所以上下两部分体积的比等于高的比。圆柱的体积为底面积×高，上部分的高可以看作(3 + 1)÷2 = 2(cm)，下部分的高可以看作(4 + 2)÷2 = 3(cm)。

2. 求长方体和圆柱组合图形的表面积。

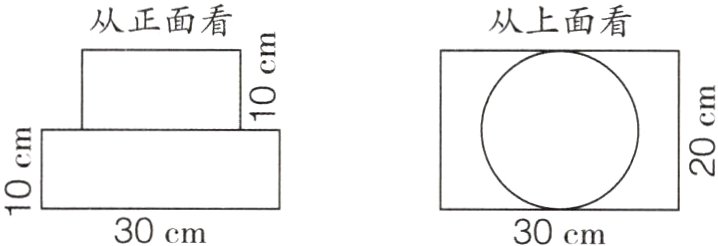
答案： (30×20 + 20×10 + 10×30)×2 + 3.14×20×10 = 2828(cm²)
解析：这个组合图形的表面积 = 长方体6个面的面积 + 圆柱的侧面积。

3. 下面的沙漏是两个完全相同的圆锥形容器的组合体，单个圆锥形容器高6cm，漏口每秒可漏细沙0.05cm³，漏完全部细沙用时5分，这个沙漏的底面积是多少平方厘米？

答案： 0.05×60×5÷$\frac{1}{3}$÷6 = 7.5(cm²)
解析：先求出沙漏5分漏出沙的体积，然后运用圆锥的体积公式的变形公式S = V÷$\frac{1}{3}$÷h，求出底面积即可。

4. 如图所示，在长方体上挖走圆柱的一半，求剩余部分的表面积和体积。(单位：cm)

答案： 10 - 4×2 = 2(cm)
表面积：(10×6 + 10×8 + 6×8)×2 + 3.14×2×6÷2 - 3.14×(2÷2)² - 6×2 = 379.7(cm²)
体积：10×6×8 - 3.14×(2÷2)²×6÷2 = 470.58(cm³)
解析：通过观察图形可知，剩余部分的表面积是原来长方体的表面积加上底面直径是(10 - 4×2)cm、高是6 cm的圆柱的侧面积的一半，再减去直径是(10 - 4×2)cm的圆的面积和一个长6 cm、宽(10 - 4×2)cm的长方形的面积；剩余部分的体积等于长方体的体积减去这个半圆柱的体积。

5. [广东深圳龙岗区期末]一个高30cm的饮料瓶中盛有饮料，如果把它倒置在桌面上(如图所示)，饮料瓶的容积是多少？(单位：cm)

答案： 3.14×(6÷2)²×(30 - 25 + 20) = 706.5(cm³)
706.5 cm³ = 706.5 mL
解析：根据图得出饮料瓶的容积就是左边饮料的体积加上右边空余部分的体积，所以饮料瓶的容积是高为30 - 25 + 20 = 25(cm)，底面直径为6 cm的圆柱的体积。

口算天天练
$\frac{2}{5}$+25%=    1.5×$\frac{2}{3}$  $\frac{6}{7}$÷2=   1÷$\frac{1}{4}$-$\frac{1}{4}$÷1=

答案： $\frac{13}{20}$   1  $\frac{3}{7}$   3$\frac{3}{4}$