《2025年核心素养天天练六年级数学下册北师大版》

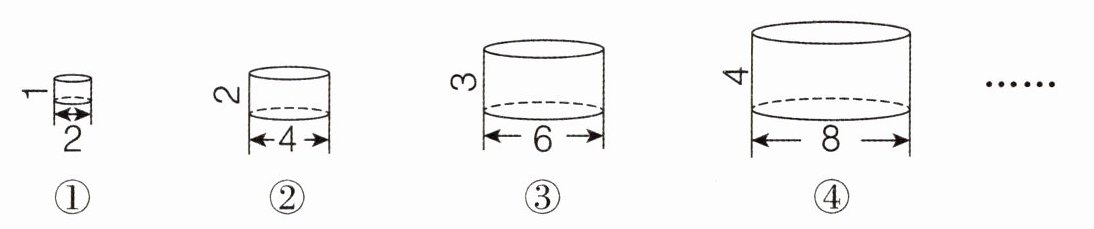
5. 观察下面的圆柱，分析它们的底面直径和高的变化引起体积变化的规律，根据这个规律,用含有字母的式子表示第n个圆柱的体积是(　　　)。

A. $\pi^{2}n$　　　　　
　B. $\pi n^{2}$　　　　　　
　C. $\pi^{2}n^{2}$　　　　　　
　D. $\pi n^{3}$

答案： D 解析：根据圆柱体积公式“$V=\pi r^{2}h$”，依次计算出图①、②、③、④的体积，据此找出规律解答即可。

1. 解方程。(16分)
250：x = 2：3　　　　　$\frac{x}{12}=\frac{3}{4}$　　　　5：0.4 = 6：x　　　　　$\frac{1}{2}:\frac{1}{3}=\frac{1}{4}:x$

答案： 250:$x$ = 2:3                       $\frac{x}{12}=\frac{3}{4}$
解：$2x = 250×3$            解：$4x = 12×3$
$2x = 750$                                  $4x = 36$
$2x\div2 = 750\div2$                    $4x\div4 = 36\div4$
$x = 375$                                   $x = 9$
5:0.4 = 6:$x$                         $\frac{1}{2}:\frac{1}{3}=\frac{1}{4}:x$
解：$5x = 0.4×6$              解：$\frac{1}{2}x=\frac{1}{3}×\frac{1}{4}$
$5x = 2.4$                                 $\frac{1}{2}x=\frac{1}{12}$
$5x\div5 = 2.4\div5$                     $\frac{1}{2}x\div\frac{1}{2}=\frac{1}{12}\div\frac{1}{2}$
$x = 0.48$                                  $x=\frac{1}{12}×2$
                                                $x=\frac{1}{6}$

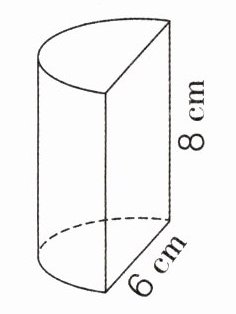
2. 计算下面图形的表面积。(5分)
　　　

答案： 3.14×(6÷2)$^{2}$+3.14×6×8÷2+6×8 = 151.62($cm^{2}$)
解析：圆柱被平均切成两半，上、下两个半圆的面积加起来等于一个圆的面积，用圆的面积公式“$S=\pi r^{2}$”求出；总的侧面积等于圆柱的侧面积的一半加上切面的面积，圆柱的侧面积可利用“$S=\pi dh$”求出，切面的面积利用长方形的面积公式“$S = ab$”求出，再把求出的面积加起来即是半个圆柱的表面积。

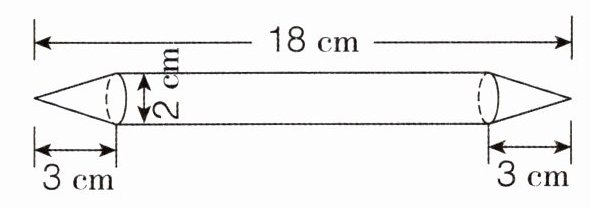
3. 计算下面图形的体积。(5分)
　　　

答案： $\frac{1}{3}×3.14×(2÷2)^{2}×3×2+3.14×(2÷2)^{2}×(18 - 3 - 3)=43.96(cm^{3})$
解析：这个组合图形是由两个完全一样的圆锥和一个圆柱组合而成，圆锥的高是3 cm，底面直径是2 cm，利用圆锥的体积公式“$V=\frac{1}{3}\pi r^{2}h$”，代入求出两个圆锥的体积，圆柱的高是(18 - 3 - 3)cm，底面直径是2 cm，再利用圆柱的体积公式“$V=\pi r^{2}h$”，求出圆柱的体积，最后把两个圆锥的体积和圆柱的体积加起来，即可求出组合图形的体积。

四、按要求操作。(共12分)
1. 将图形①绕点O逆时针旋转90°。(3分)
2. 将图形①先向上平移3格,再向右平移4格,得到图形②。(3分)
3. 以虚线为对称轴,画出图形②的轴对称图形③。(3分)
4. 将图形①放大得到图形④,使放大后的图形与原图形对应线段长的比是2：1。(3分)
　　　　　　

答案：