《2025年核心素养天天练六年级数学下册北师大版》

1. 下面每题中的两个量是否成比例？成什么比例？并说明理由。
（1）作业数量一定，完成的与没有完成的。
（2）织布的总长度一定，平均每时织布的长度和时间。
（3）购买服装的总价一定，服装的单价和数量。

答案：
(1)完成的作业量+没有完成的作业量=作业总数量，作业总数量一定，即和一定，所以完成的与没有完成的不成比例。
(2)平均每时织布的长度×时间=织布的总长度(一定)，所以平均每时织布的长度和时间成反比例。
(3)服装的单价×数量=总价(一定)，所以服装的单价和数量成反比例。
解析：两个相关联的量之间如果是比值一定，就成正比例；如果是乘积一定，则成反比例。

2. 食品店运来36个面包，需要平均装入小袋子里，可以怎么装？（一个袋子内的面包数量小于或等于6）
　　　　
从表中，你能发现小袋子的数量与每袋面包数量有怎样的关系吗？请说明理由。

答案： 每袋面包数量/个：6、4、3、2、1；小袋子数量/个：6、9、12、18、36。小袋子的数量与每袋面包数量的乘积一定，成反比例。
解析：依据一个袋子内的面包数量小于或等于6，故可设每袋面包数量分别为：1、2、3、4、6个，然后依据数量关系：面包总数÷每袋面包数量=小袋子数量进行计算填表；判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定。

3.（1）如果要一次运出120t救灾物资，车辆的载质量与所需车辆的数量如下表。请把表格填写完整。

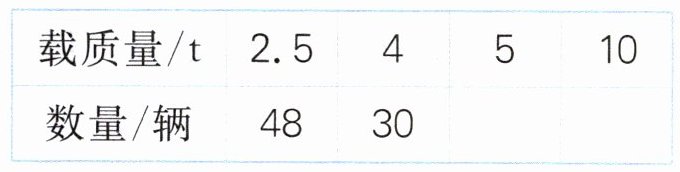
①车辆的载质量和所需车辆的数量成什么比例？为什么？
②如果用载质量6t的卡车来运，一共需要多少辆？

（2）如果用8辆载质量是2.5t的卡车来运，运输的次数和所运救灾物资的数量如下表。请把表格填写完整。运输的次数和所运物资的质量成什么比例？为什么?
　　　　　　　　　　　　　　　　

答案：
(1)24 12
①成反比例，因为车辆的载质量和所需车辆的数量的乘积一定。
②120÷6 = 20(辆)
(2)20 40 60 80 100 120
成正比例，因为运输的次数和所运物资的质量的比值一定。
解析：
(1)车辆的载质量和所需车辆的数量的乘积一定，120÷5 = 24，120÷10 = 12。
(2)2.5×8 = 20(t)，2×20 = 40，3×20 = 60，4×20 = 80，5×20 = 100，6×20 = 120。

4. 如果$\frac{x}{2}=\frac{3}{y}$，那么$x$和$y$成什么比例？如果$2x = 3y$，那么$x$和$y$成什么比例？

答案： 反比例 正比例
解析：$\frac{x}{2}=\frac{3}{y}$变形为$xy = 6$，乘积一定，所以$x$和$y$成反比例；$2x = 3y$可变形为$x:y=\frac{3}{2}$，比值一定，所以$x$和$y$成正比例。

口算天天练
2022+88=   ($\frac{5}{6}$+$\frac{2}{9}$)×54=  1÷$\frac{1}{9}$×9=  1+2%=  4.8÷24=

答案： 2110  57  81  1.02  0.2