《2025年核心素养天天练六年级数学下册北师大版》

1. 填一填。
(1)一个底面周长为4 cm的圆柱侧面展开后是一个正方形，这个圆柱的高是(　　　)cm，这个正方形的面积是(　　　)cm²。

答案：
(1)4 16 解析：圆柱的侧面展开后是正方形，说明圆柱的底面周长等于高。底面周长为4cm，则这个圆柱的高也是4cm。展开后的正方形的面积就是圆柱的侧面积，圆柱的侧面积 = 底面周长×高，据此代入数据计算。

(2)做8个直径4 dm、高5 dm的通风管，需要(　　　)dm²铁皮。

答案：
(2)502.4 解析：由题意知，求通风管的面积就是求圆柱的侧面积，利用圆柱的侧面积公式S = πdh，计算出一个通风管的侧面积，再乘8即可。

(3)一个底面半径是5 cm，高是8 cm的圆锥，若沿高切割，表面积增加(　　　)cm²。

答案：
(3)80 解析：根据题意可知，一个底面半径是5cm，高是8cm的圆锥，若沿高切割，表面积增加两个以圆锥的高为高，圆锥的底面直径为底的三角形的面积，根据三角形的面积公式S = ah÷2，把数据代入公式解答。

(4)一个圆柱形容器，从里面量，底面直径是10 cm，高是5 cm，它的容积是(　　　)mL。

答案：
(4)392.5 解析：根据圆柱的容积 = 底面积×高，代入数据，即可解答。

2. [广东深圳龙华区期末]求下面图形的表面积或体积。

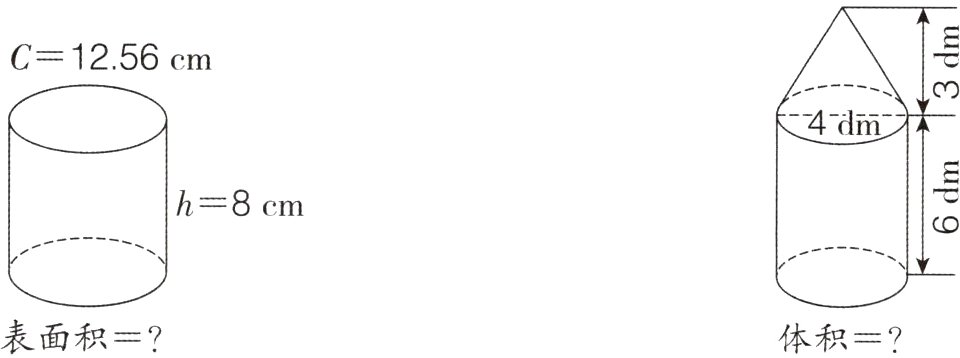
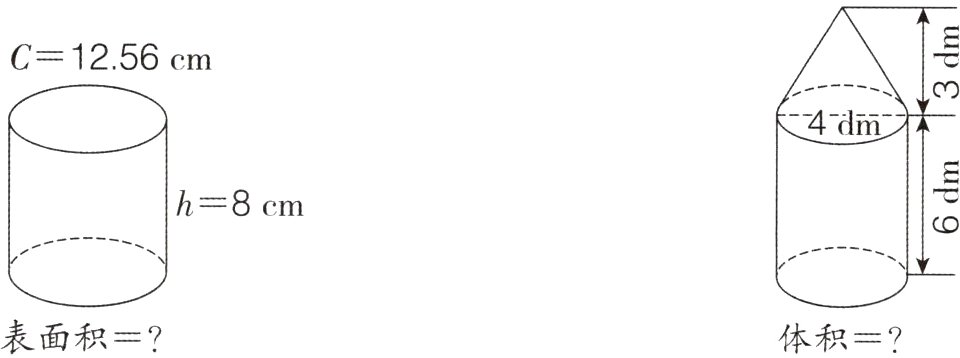
答案： 12.56×8 + 3.14×(12.56÷3.14÷2)²×2 = 125.6(cm²)
3.14×(4÷2)²×6 + $\frac{1}{3}$×3.14×(4÷2)²×3 = 87.92(dm³)
解析：圆柱的表面积 = 侧面积 + 底面积×2，圆柱的体积公式：V = πr²h，圆锥的体积公式：V = $\frac{1}{3}$πr²h。

3. [河南漯河源汇区期末]砌一个圆柱形的沼气池，底面直径是2 m，深是5 m，在沼气池的周围和下面的底面抹上水泥，抹水泥部分的面积是多少平方米？这个沼气池可以容纳多少立方米的沼气?

答案： 3.14×2×5 + 3.14×(2÷2)² = 34.54(m²)
3.14×(2÷2)²×5 = 15.7(m³)
解析：抹水泥的面积是这个圆柱的侧面积与一个底面积的和，侧面积 = 底面周长×高，底面积 = πr²，可代入数据求出抹水泥的面积；根据圆柱的体积公式V = πr²h，求出这个沼气池的容积。

4. [湖北潜江期末]故宫博物院馆藏“碧玉刻诗扳指”(如图)，器呈圆筒状。直径2.90 cm，高2.20 cm，厚0.50 cm。外部雕填金地萱花一枝。另一侧有填金《御题萱花诗》一首：“叶绿与花黄，无情自在芳。持将赠屈子，定是不能忘。”则这枚扳指的体积是多少立方厘米？(得数保留两位小数)

答案： 2.90÷2 = 1.45(cm) 1.45 - 0.50 = 0.95(cm)
3.14×1.45²×2.20 - 3.14×0.95²×2.20≈8.29(cm³)
解析：根据圆柱的体积 = 底面积×高，用外圆柱的体积减去内圆柱的体积即可。

5. [湖北武汉洪山区期末]圆柱如下图切拼成长方体后表面积比原来增加了20 cm²，原来圆柱的侧面积是多少平方厘米？

答案： 20×3.14 = 62.8(cm²)
解析：由图可知，长方体的长等于圆柱底面周长的一半，长方体的宽等于圆柱的底面半径，长方体的高等于圆柱的高，增加部分的面积 = 圆柱的底面半径×高×2，圆柱的侧面积公式为S侧 = 2πrh，根据增加部分的面积求出圆柱的侧面积即可。

口算天天练
3÷10%=    0.4³=   ($\frac{5}{6}$-$\frac{3}{4}$)×24=   $\frac{4}{7}$+$\frac{5}{11}$+$\frac{3}{7}$-$\frac{6}{11}$=

答案： 30  0.064   2  $\frac{10}{11}$