《2025年核心素养天天练六年级数学下册北师大版》

1. 填一填。
(1)在△ABC中，∠A：∠B：∠C = 2：3：4，则∠A =（ ）°，按角的大小分类，这个三角形是（ ）三角形。

答案：
(1)40 锐角 解析：三角形内角和等于180°，内角和÷总份数 = 一份数，一份数×∠A对应份数 = ∠A度数，一份数×∠C对应份数 = ∠C度数，根据三角形分类标准，确定三角形类型即可。

(2)[北京丰台区期末]用长4 cm、宽3 cm的长方形密铺成一个正方形，至少需要（ ）个这样的长方形。

答案：
(2)12 解析：先求出正方形的边长最小是多少厘米，即求4和3的最小公倍数；然后根据求出的正方形的边长进行分析：看能放几排，几列，最后相乘即可。

(3)[福建莆田城厢区期末]小明有3 cm、4 cm、5 cm的小棒若干根，他设计了如下的拼图方案:

照这样拼下去，第⑥个图形的周长是（ ）cm，需要小棒（ ）根；第⑦个图形的周长是（ ）cm；第a个图形需要小棒（ ）根。

答案：
(3)26 13 30 2a + 1 解析：第①个图形需要3根小棒，第②个图形需要(3 + 2×1)根小棒，第③个图形需要(3 + 2×2)根小棒，第④个图形需要(3 + 2×3)根小棒，第⑤个图形需要(3 + 2×4)根小棒……每增加一个三角形就增加2根小棒，据此表示第a个图形需要小棒的根数；第①个图形的周长为(3 + 4 + 5)cm，第②个图形的周长为(3 + 4)×2 cm，第③个图形的周长为(3 + 4 + 5 + 3×2)cm，第④个图形的周长为(3×2 + 4)×2 cm，第⑤个图形的周长为(3 + 4 + 5 + 3×4)cm，第⑥个图形的周长为(3×3 + 4)×2 cm，第⑦个图形的周长为(3 + 4 + 5 + 3×6)cm，据此解答。

2. 淘气为了估测学校喷泉两边A、B之间的距离(如图)，在喷泉的一侧选取一点O，测得OA = 9 m，OB = 6 m。根据以上信息，淘气说：“A、B之间的距离不可能是16 m。”你认为淘气说得对吗？请写出你的理由。

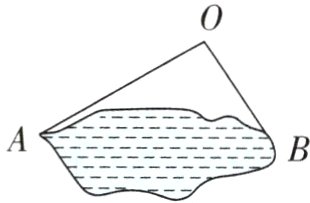
答案： 淘气说得对。
9 - 6＜A、B之间的距离＜9 + 6
3＜A、B之间的距离＜15
即A、B之间的距离取值在3～15 m(不包括3 m和15 m)，所以A、B之间的距离不可能是16 m，淘气说得对。
解析：根据“三角形三边关系：任意两边之和大于第三边，三角形的任意两边的差一定小于第三边”进行解答即可。

3. 用两根长54 cm的铁丝分别围成一个等腰三角形和一个等边三角形，已知等腰三角形的腰长16 cm，底长是多少厘米？等边三角形的边长是多少厘米？

答案： 底：54 - 16×2 = 22(cm)
边长：54÷3 = 18(cm)
解析：等腰三角形的两腰相等，用周长减去2个腰长即可求出底边的长度；等边三角形的三条边相等，用54除以3就是这个等边三角形的边长。

4. 按要求画图。

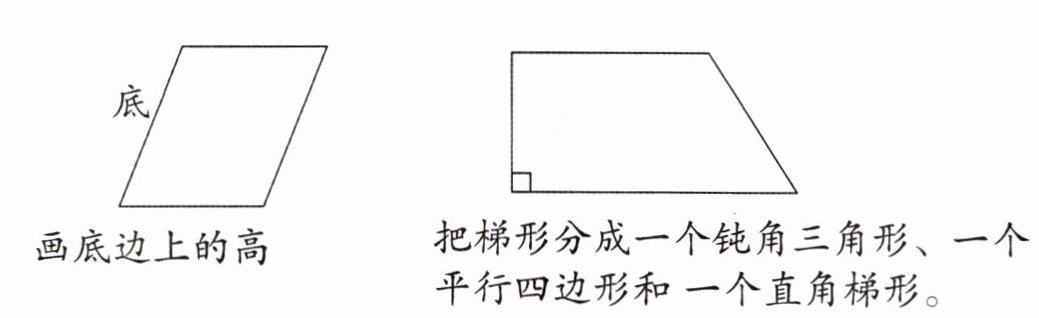
答案：
(答案不唯一)
　　　

5. AB是一条直线，可向两端延伸，OC是线段，长度确定，以OC为一条边，在AB上找一点D，使得△OCD是等腰三角形，这样的点D有几个？

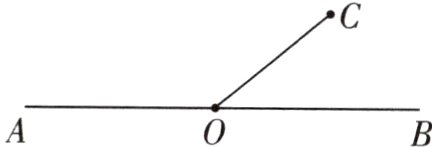
答案：
当OC为底时，则作OC的垂直平分线，交AB有一点，所以有1个。
当OC为腰时，以点O为圆心，OC为半径画圆，交AB有两点，所以有2个；当以点C为圆心，CO为半径画圆，交AB有一点，所以有1个。
1 + 2 + 1 = 4(个)

解析：根据等腰三角形的定义和性质，在平面图中找出所有符合题意的点即可。

口算天天练
1÷0.5×3.5=   3÷0.9=   9.9x 100%=   100x9.8+0.2=

150%÷25%=  9÷8=    0.2+49x0.2=    125x9x0.8=

答案： 口算天天练：7 $\frac{10}{3}$ 9.9 980.2   6   $\frac{9}{8}$ 10 900