《2025年核心素养天天练六年级数学下册北师大版》

1. 下表是乐乐0～9岁的体重变化情况，发生变化的两个量是( )和( )。
　　　　　

答案： 年龄 体重 解析：根据图表可得乐乐的体重随着年龄的变化而变化。

2. 已知x和y所成的比例关系，可以用y = 5x表示，根据这个关系先填写下表，再回答问题。
　　
x和y所表示的两个量成( )比例。

答案： 10 20 30 40 50 60 70 80 正
解析：$y = 5x$，说明$y$是$x$的5倍，由此用表格中$x$的值乘5即可依次求出$y$的值；根据数量判断二者的商一定，成正比例。

3. 大白鲨2时游140 km，照这样的速度，大白鲨12时游( )km，一昼夜能游( )km。

答案： 840 1680 解析：“照这样的速度”，即路程：时间 = 速度(比值一定)，根据大白鲨所游的路程与时间的比值一定及比例的性质分别求出12时所游的路程、一昼夜所游的路程即可。

4. 甲、乙两个数，如果能使等式甲×4 = 乙÷$\frac{1}{20}$成立，那么甲和乙成( )比例。

答案： 正 解析：因为甲×4 = 乙÷$\frac{1}{20}$，所以甲×4 = 乙×20，$\frac{甲}{乙}$ = $\frac{20}{4}$ = 5，甲和乙比值一定，成正比例。

5. 如图，x和y是两个相关联的量。当x = 2时，y =( )；当y = 40时，x =( )。x和y成( )比例。
　　　　　　　　　　　　　　　　　　　　　　　　　　

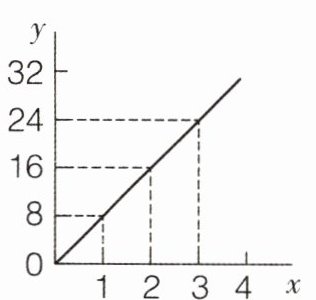
答案： 16 5 正 解析：观察题中数据图可知，$y$与$x$是相关联的两个量，且$y$与$x$相对应的数的比值等于8(比值一定)，$x$和$y$成正比例。

6. 平行四边形的底和高的关系如图所示。当底是40 cm时，高是( )cm；当高是10 cm时，底是( )cm。底和高成( )比例。平行四边形相邻两边( )比例。
　　　　　　　　　　　　　　　　　　　　　　　　　　　

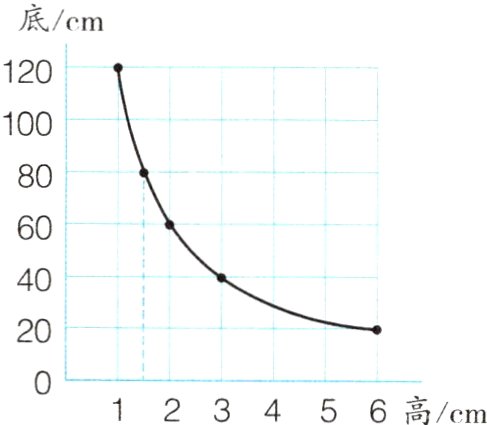
答案： 3 12 反 不成 解析：120×1 = 120($cm^{2}$)，80×1.5 = 120($cm^{2}$)，所以120÷40 = 3(cm)，120÷10 = 12(cm)，底×高 = 平行四边形的面积(一定)，底和高成反比例；平行四边形相邻两边不成比例。

1. 下面几种情况中，成反比例的是( )。
A. 每公顷的产量一定，总产量和公顷数
B. 一根绳子，剪去的一段和剩下的一段
C. 三角形的面积一定，底和相对应的高
D. 圆的面积一定，圆周率和半径

答案： C 解析：两个相关联的量，比值一定，就成正比例；乘积一定，就成反比例，除此以外，不成比例。

2. [贵州遵义播州区期末]正方形的周长和它的边长( )。
A. 成正比例 B. 成反比例 C. 不成比例 D. 无法确定

答案： A 解析：正方形的周长÷边长 = 4，两个相关联的量比值一定，成正比例。

3. 下面( )图中的两个变量是成正比例的量。
　　

答案： A 解析：正比例图象是一条直线，且变化趋势一致；反比例图象是一条曲线，且变化方向相反，据此判断。