《2025年综合应用创新题典中点九年级数学下册冀教版》

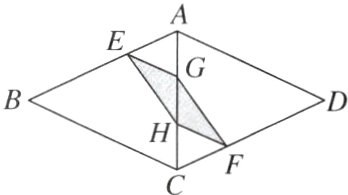
8. 如图，小球在菱形ABCD中自由地滚动，点E，F分别在AB，CD上，且BE = 2AE，DF = 2CF，点G，H在AC上，且AG = GH = CH，则小球最终停在阴影区域中的概率是________.

答案： $\frac{1}{9}$ 【点拨】$\because BE = 2AE$，$DF = 2FC$，$\therefore\frac{AE}{BE}=\frac{1}{2}$，$\frac{CF}{DF}=\frac{1}{2}$. $\because AG = GH = CH$，$\therefore\frac{AG}{GC}=\frac{1}{2}$. $\therefore\frac{AE}{EB}=\frac{AG}{GC}$. $\therefore\frac{AE}{AB}=\frac{AG}{AC}$. 又$\because\angle EAG=\angle BAC$，$\therefore\triangle AEG\backsim\triangle ABC$. $\therefore\frac{S_{\triangle AEG}}{S_{\triangle ABC}}=(\frac{AE}{AB})^2=\frac{1}{9}$. 同理可得$\frac{S_{\triangle CFH}}{S_{\triangle CDA}}=(\frac{CH}{AC})^2=\frac{1}{9}$. 易得$S_{\triangle AEG}=S_{\triangle HEG}$，$S_{\triangle CFH}=S_{\triangle GFH}$，$\therefore\frac{S_{四边形EGFH}}{S_{菱形ABCD}}=\frac{S_{\triangle AEG}+S_{\triangle CFH}}{S_{\triangle ABC}+S_{\triangle ACD}}=\frac{1}{9}$. $\therefore$小球最终停在阴影区域中的概率是$\frac{1}{9}$.

9. 某商场为了吸引顾客，设立了一个可以自由转动的转盘（如图，转盘被均匀分为20份，扇形中所写文字代表该扇形所涂的颜色），并规定：顾客每购物满100元，就能获得一次转动转盘的机会. 如果转盘停止后，指针正好对准红色、黄色、绿色区域，顾客就可以分别获得100元、50元、20元的购物券. 为加大促销力度，超市决定在原转盘的基础上将空白的扇形涂色来增大顾客获得购物券的概率. 若要使每次转动转盘获得购物券的概率为$\frac{9}{20}$，且获得100元、50元、20元购物券的概率之比为1∶3∶5，则需要涂成红色、黄色、绿色的空白扇形分别是几个？

答案： 【解】$\because20\times\frac{9}{20}=9$(个)，$\therefore$涂成红色、黄色、绿色的扇形共有9个. $\because$获得100元、50元、20元购物券的概率之比为1:3:5，$\therefore$涂成红色、黄色、绿色的扇形的个数之比为1:3:5. $\therefore$涂成红色、黄色、绿色的扇形的个数分别为1，3，5，$\therefore$需要涂成红色、黄色、绿色的空白扇形的个数分别是0，1，1.

10. 有一张原创儿童剧《长安在哪里》的门票，小明和小亮都想得到它，小红为他们设计了一个游戏：从牌面为1（A），2，3，4，4，5，6，7的8张扑克牌中任取一张，抽到比4大的，小明去；否则，小亮去.
（1）求小明抽到4的概率.
（2）你认为这个游戏对小明和小亮公平吗？若公平，请说明理由；若不公平，请你修改游戏规则，使游戏对双方都公平.

答案： 【解】
(1)因为所有可能出现的结果一共有8种，其中抽到4的结果有2种，故小明抽到4的概率为$\frac{2}{8}=\frac{1}{4}$.
(2)不公平. 修改游戏规则如下：从牌面为1(A)，2，3，4，5，4，6，7的8张扑克牌中任取一张，抽到比4大的，小明去；抽到比4小的，小亮去；抽到4则重新抽. (答案不唯一)

11. 母题 教材P65A组T4 如图是计算机“扫雷”游戏的画面，在9×9个小方格的雷区中，随机埋藏着20颗地雷，每个小方格最多能埋藏1颗地雷. 小林和小艾轮流点击，小林先点一个小方格，显示数字2，它表示围着数字2的8个方格中埋藏着2颗地雷（包含数字2的黑框区域记为A）.
（1）若小艾在区域A中围着数字2的8个方格中任点一个，未踩中地雷的概率是多少？
（2）现在小艾点击了右下角的一个方格，出现了数字1（包含数字1的黑框区域记为B），轮到小林点击，若小林打算在区域A和区域B中任点一个未点击的方格，从安全的角度考虑，他应该选择哪个区域？

答案： 【解】
(1)$\because$区域A中围着数字2的8个方格中埋藏着2颗地雷，$\therefore$有6个方格没有地雷. $\therefore$未踩中地雷的概率是$\frac{6}{8}=\frac{3}{4}$.
(2)由
(1)知，区域A中未踩中地雷的概率是$\frac{3}{4}$，$\because$区域B中除1外的3个方格中埋着1颗地雷，有2个方格没有地雷，$\therefore$区域B中未踩中地雷的概率是$\frac{2}{3}$. $\because\frac{3}{4}＞\frac{2}{3}$，$\therefore$从安全的角度考虑，他应该选择区域A.