第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
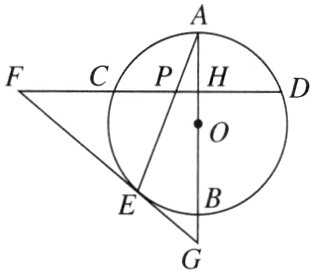
8. 如图,在⊙O中,AB是直径,弦CD⊥AB,垂足为H,E为$\overset{\frown}{BC}$上一点,F为弦DC延长线上一点,连接FE并延长交直径AB的延长线于点G,连接AE交CD于点P,FE = FP.
(1)求证:FE是⊙O的切线;
(2)若⊙O的半径为8,sin F = $\frac{3}{5}$,求BG的长.
(1)求证:FE是⊙O的切线;
(2)若⊙O的半径为8,sin F = $\frac{3}{5}$,求BG的长.

答案:
(1)[证明]如图,连接OE.
∵OA=OE,
∴∠A=∠AEO.
∵CD⊥AB,
∴∠AHP=90°,
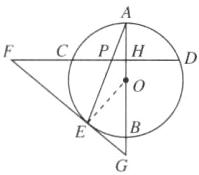
∵FE=FP,
∴∠FPE=∠FEP.
∵∠APH=∠FPE,
∴∠A+∠FPE=∠A+∠APH=90°,
∴∠FEP+∠AEO=90°=∠FEO.
∴OE⊥EF.又
∵OE为⊙O的半径,
∴FE是⊙O的切线.
(2)[解]
∵∠FHG=∠OEG=90°,
∴∠G+∠EOG=90°=∠G+∠F.
∴∠F=∠EOG.
∴sin∠EOG=$\frac{EG}{OG}$=sinF=$\frac{3}{5}$.
∴设EG=3x,则OG=5x,
∴OE=$\sqrt{OG^{2}-EG^{2}}$=$\sqrt{25x^{2}-9x^{2}}$=4x.
∵OE=8,
∴4x=8,解得x=2.
∴OG=10.
∴BG=OG−OB=10−8=2.
(1)[证明]如图,连接OE.
∵OA=OE,
∴∠A=∠AEO.
∵CD⊥AB,
∴∠AHP=90°,

∵FE=FP,
∴∠FPE=∠FEP.
∵∠APH=∠FPE,
∴∠A+∠FPE=∠A+∠APH=90°,
∴∠FEP+∠AEO=90°=∠FEO.
∴OE⊥EF.又
∵OE为⊙O的半径,
∴FE是⊙O的切线.
(2)[解]
∵∠FHG=∠OEG=90°,
∴∠G+∠EOG=90°=∠G+∠F.
∴∠F=∠EOG.
∴sin∠EOG=$\frac{EG}{OG}$=sinF=$\frac{3}{5}$.
∴设EG=3x,则OG=5x,
∴OE=$\sqrt{OG^{2}-EG^{2}}$=$\sqrt{25x^{2}-9x^{2}}$=4x.
∵OE=8,
∴4x=8,解得x=2.
∴OG=10.
∴BG=OG−OB=10−8=2.
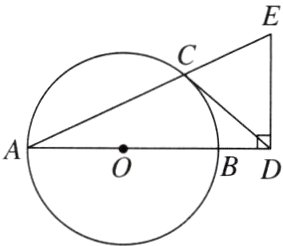
9. 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC = DE;
(2)若tan∠CAB = $\frac{1}{2}$,AB = 3,求BD的长.
(1)求证:DC = DE;
(2)若tan∠CAB = $\frac{1}{2}$,AB = 3,求BD的长.

答案:
(1)[证明]连接OC,如图,
∵CD与⊙O相切于点C,
∴∠OCD=90°.
∴∠ACO+∠DCE=90°.
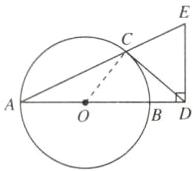
∵ED⊥AD,
∴∠EDA=90°.
∴∠EAD+∠E=90°.
∵OC=OA,
∴∠ACO=∠EAD,
∴∠DCE=∠E.
∴DC=DE.
(2)[解]设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x.在Rt△EAD中,
∵tan∠CAB=$\frac{1}{2}$,
∴ED=$\frac{1}{2}$AD=$\frac{1}{2}$(3+x).
∴DC=DE=$\frac{1}{2}$(3+x).
在Rt△OCD中,OC²+CD²=DO²,
则1.5²+[$\frac{1}{2}$(3+x)]²=(1.5+x)²,
解得x₁=−3(舍去),x₂=1,
∴BD=1.
(1)[证明]连接OC,如图,
∵CD与⊙O相切于点C,
∴∠OCD=90°.
∴∠ACO+∠DCE=90°.

∵ED⊥AD,
∴∠EDA=90°.
∴∠EAD+∠E=90°.
∵OC=OA,
∴∠ACO=∠EAD,
∴∠DCE=∠E.
∴DC=DE.
(2)[解]设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x.在Rt△EAD中,
∵tan∠CAB=$\frac{1}{2}$,
∴ED=$\frac{1}{2}$AD=$\frac{1}{2}$(3+x).
∴DC=DE=$\frac{1}{2}$(3+x).
在Rt△OCD中,OC²+CD²=DO²,
则1.5²+[$\frac{1}{2}$(3+x)]²=(1.5+x)²,
解得x₁=−3(舍去),x₂=1,
∴BD=1.
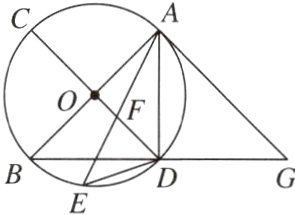
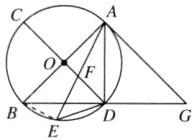
10. [2024北京海淀区模拟] 如图,AB,CD均为⊙O的直径,点E在$\overset{\frown}{BD}$上,连接AE,交CD于点F,连接DE,AD. ∠EDB + ∠EAD = 45°,点G在BD的延长线上,AB = AG.
(1)求证:AG与⊙O相切;
(2)若BG = 4$\sqrt{5}$,tan∠EDB = $\frac{1}{3}$,求EF的长.
(1)求证:AG与⊙O相切;
(2)若BG = 4$\sqrt{5}$,tan∠EDB = $\frac{1}{3}$,求EF的长.

答案:
(1)[证明]
∵∠EDB+∠EAD=45°,∠EDB=∠EAB,
∴∠EAB+∠EAD=45°=∠BAD.
∵AB为⊙O的直径,
∴∠ADB=90°.
又
∵AB=AG,
∴∠GAD=∠BAD=45°.
∴∠GAB=90°.
∴AB⊥AG.
又
∵OA为⊙O的半径,
∴AG与⊙O相切.
(2)[解]如图,连接BE,
由
(1)易知BD=$\frac{1}{2}$BG=2$\sqrt{5}$
∴易得AB=$\sqrt{2}$BD=2$\sqrt{10}$.
∴OA=$\sqrt{10}$
∵AB为⊙O的直径,
∴∠BEA=90°.
∴$\frac{BE}{AE}$=tan∠EAB=tan∠EDB=$\frac{1}{3}$.
∴BE=$\frac{1}{3}$AE.
在Rt△ABE中,BE²+AE²=AB²,
∴($\frac{1}{3}$AE)²+AE²=(2$\sqrt{10}$)²,
解得AE=6(负值已舍去).
∵∠BOD=2∠BAD=90°,
∴∠AOF=90°.
∴$\frac{OF}{OA}$=tan∠EAB=$\frac{1}{3}$.
∴OF=$\frac{1}{3}$OA=$\frac{\sqrt{10}}{3}$.
∴AF=$\sqrt{OA^{2}+OF^{2}}$=$\frac{10}{3}$.
∴EF=AE−AF=$\frac{8}{3}$.
(1)[证明]
∵∠EDB+∠EAD=45°,∠EDB=∠EAB,
∴∠EAB+∠EAD=45°=∠BAD.
∵AB为⊙O的直径,
∴∠ADB=90°.
又
∵AB=AG,
∴∠GAD=∠BAD=45°.
∴∠GAB=90°.
∴AB⊥AG.
又
∵OA为⊙O的半径,
∴AG与⊙O相切.
(2)[解]如图,连接BE,
由
(1)易知BD=$\frac{1}{2}$BG=2$\sqrt{5}$
∴易得AB=$\sqrt{2}$BD=2$\sqrt{10}$.
∴OA=$\sqrt{10}$
∵AB为⊙O的直径,
∴∠BEA=90°.
∴$\frac{BE}{AE}$=tan∠EAB=tan∠EDB=$\frac{1}{3}$.
∴BE=$\frac{1}{3}$AE.
在Rt△ABE中,BE²+AE²=AB²,
∴($\frac{1}{3}$AE)²+AE²=(2$\sqrt{10}$)²,
解得AE=6(负值已舍去).

∵∠BOD=2∠BAD=90°,
∴∠AOF=90°.
∴$\frac{OF}{OA}$=tan∠EAB=$\frac{1}{3}$.
∴OF=$\frac{1}{3}$OA=$\frac{\sqrt{10}}{3}$.
∴AF=$\sqrt{OA^{2}+OF^{2}}$=$\frac{10}{3}$.
∴EF=AE−AF=$\frac{8}{3}$.
查看更多完整答案,请扫码查看


