《2025年综合应用创新题典中点九年级数学下册冀教版》

8. 已知点$(x_{1},y_{1})$，$(x_{2},y_{2})$均在抛物线$y=x^{2}-1$上，下列说法中正确的是 （ ）
A. 若$y_{1}=y_{2}$，则$x_{1}=x_{2}$
B. 若$x_{1}=-x_{2}$，则$y_{1}=-y_{2}$
C. 若$0 ＜ x_{1}＜x_{2}$，则$y_{1}＞y_{2}$
D. 若$x_{1}＜x_{2}＜0$，则$y_{1}＞y_{2}$

答案：
D 【点拨】若$y_{1}=y_{2}$，则$x_{1}^{2}-1=x_{2}^{2}-1$，
∴$x_{1}=x_{2}$或$x_{1}=-x_{2}$，
∴选项A是错误的；若$x_{1}=-x_{2}$，则$x_{1}^{2}=x_{2}^{2}$，
∴$x_{1}^{2}-1=x_{2}^{2}-1$，
∴$y_{1}=y_{2}$，
∴选项B是错误的；如图，抛物线$y = x^{2}-1$的对称轴是$y$轴，在对称轴的左侧，$y$随$x$的增大而减小；在

对称轴的右侧，$y$随$x$的增大而增大.
∴若$0＜x_{1}＜x_{2}$，则$y_{1}＜y_{2}$，若$x_{1}＜x_{2}＜0$，则$y_{1}＞y_{2}$，
∴选项C是错误的，选项D是正确的. 故选D.

9. 如图，在平面直角坐标系中，抛物线$y = ax^{2}+6$与$y$轴交于点$A$，过点$A$与$x$轴平行的直线交抛物线$y = 2x^{2}$于$B$，$C$两点，则$BC$的长为 （ ）

A. $\sqrt{2}$
B. $\sqrt{3}$
C. $2\sqrt{2}$
D. $2\sqrt{3}$

答案： D 【点拨】对于$y = ax^{2}+6$，当$x = 0$时，$y = 6$，
∴点A的坐标为(0，6).
由题意得A，B，C三点在同一直线上，且$BC// x$轴，
∴B，C两点的纵坐标均为6. 对于$y = 2x^{2}$，当$y = 6$时，$2x^{2}=6$，解得$x = \pm\sqrt{3}$，
∴点B的坐标为$(-\sqrt{3},6)$，点C的坐标为$(\sqrt{3},6)$.
∴$BC=\sqrt{3}-(-\sqrt{3})=2\sqrt{3}$.

10. [新视角 新定义型题] 若抛物线$y = ax^{2}+c$与$x$轴交于点$A(m,0)$，$B(n,0)$，与$y$轴交于点$C(0,c)$，则称$\triangle ABC$为“抛物三角形”. 特别地，当$mnc ＜ 0$时，称$\triangle ABC$为“倒抛物三角形”，此时$a$，$c$应分别满足的条件为 （ ）
A. $a＞0$，$c＞0$
B. $a＞0$，$c＜0$
C. $a＜0$，$c＞0$
D. $a＜0$，$c＜0$

答案： C 【点拨】
∵抛物线$y = ax^{2}+c$的对称轴是$y$轴，
∴$A(m,0)$，$B(n,0)$关于$y$轴对称.
∴$mn＜0$. 又
∵$mnc＜0$，
∴$c＞0$，即抛物线与$y$轴的正半轴相交. 又
∵抛物线$y = ax^{2}+c$与$x$轴有两个交点，
∴抛物线开口向下.
∴$a＜0$.

11. [新考法 割补法] 如图，两条抛物线$y_{1}=-\frac{1}{2}x^{2}+1$，$y_{2}=-\frac{1}{2}x^{2}-1$与分别经过点$(-2,0)$，$(2,0)$且平行于$y$轴的两条平行线围成的阴影部分的面积为_______.

答案：
8 【点拨】如图，过抛物线$y_{2}=-\frac{1}{2}x^{2}-1$的顶点(0，-1)且平行于$x$轴的直线与抛物线$y_{1}=-\frac{1}{2}x^{2}+1$围成的阴影(记为阴影A)，与过点(0，-3)且平行于$x$轴的直线与抛物线$y_{2}=-\frac{1}{2}x^{2}-1$围成的图形形状、大小相同，故把阴影A向下平移2个单位长度即可与剩余的阴影拼成一个矩形，易知矩形的面积为$4×2 = 8$，
∴所求阴影部分的面积为8.

12. 若关于$x$的二次函数$y = ax^{2}+a^{2}$，当$-1\leqslant x\leqslant\frac{1}{2}$时，$y$有最大值6，则$a =$_______.

答案： 2或$-\sqrt{6}$ 【点拨】若$a＜0$，易知当$x = 0$时，$y$取最大值，最大值为$a^{2}$，
∴$a^{2}=6$，解得$a=\sqrt{6}$(舍去)或$a = -\sqrt{6}$；若$a＞0$，易知当$x=-1$时，$y$取最大值，最大值为$a + a^{2}$，
∴$a + a^{2}=6$，解得$a = 2$或$a=-3$(舍去).
综上所述，$a = 2$或$a = -\sqrt{6}$.

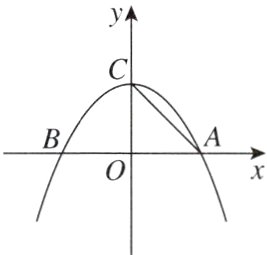
13. [新视角 存在性探究题] 如图，抛物线$y=-\frac{1}{2}x^{2}+2$与$x$轴交于$A$，$B$两点，其中点$A$在$x$轴的正半轴上，点$B$在$x$轴的负半轴上.
（1）试写出该抛物线的对称轴和顶点$C$的坐标.
（2）在抛物线上是否存在一点$M$，使$\triangle MAC\cong\triangle OAC$？若存在，求出点$M$的坐标；若不存在，请说明理由.

答案： 【解】
(1)
∵抛物线的表达式为$y=-\frac{1}{2}x^{2}+2$，
∴抛物线的对称轴是$y$轴，当$x = 0$时，$y = 2$，
∴抛物线的顶点C的坐标为(0，2).
(2)不存在. 理由如下：
∵抛物线$y=-\frac{1}{2}x^{2}+2$与$x$轴正半轴交于点A，
∴易得$A(2,0)$.
又
∵$C(0,2)$，
∴$OA = OC = 2$.
又
∵$\angle AOC = 90^{\circ}$，
∴$\triangle OAC$是等腰直角三角形.
假设抛物线上存在一点M使$\triangle MAC\cong\triangle OAC$，
∵AC为公共边，$OA = OC$，
∴易得点M与点O关于直线AC对称，
∴$M(2,2)$.
当$x = 2$时，$y=-\frac{1}{2}×2^{2}+2 = 0≠2$.
∴点M不在抛物线上.
∴不存在这样的点M.

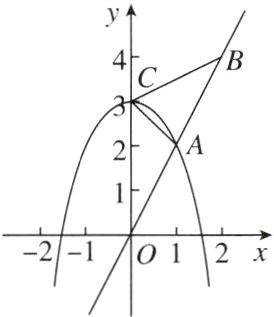
14. [2024天津南开区期中] 如图，已知正比例函数$y = 2x$的图像与抛物线$y = ax^{2}+3$相交于点$A(1,b)$.
（1）求$a$，$b$的值；
（2）若点$B(m,4)$在函数$y = 2x$的图像上，抛物线$y = ax^{2}+3$的顶点是$C$，求$\triangle ABC$的面积；
（3）若点$P$是$x$轴上的一个动点，求当$PA + PC$的值最小时点$P$的坐标.

答案： 【解】
(1)
∵点$A(1,b)$在正比例函数$y = 2x$的图像上，
∴$b = 2×1 = 2$.
∴$A(1,2)$.
∵点$A(1,2)$在抛物线$y = ax^{2}+3$上，
∴$2 = a×1^{2}+3$，解得$a=-1$.
(2)
∵点$B(m,4)$在函数$y = 2x$的图像上，
∴$4 = 2m$，解得$m = 2$.
∴$B(2,4)$.
∵抛物线$y=-x^{2}+3$的顶点是C，且当$x = 0$时，$y = 3$，
∴$C(0,3)$.
∵点A的坐标为(1，2)，
∴$S_{\triangle ABC}=S_{\triangle OBC}-S_{\triangle OAC}=\frac{1}{2}×3×2-\frac{1}{2}×3×1=\frac{3}{2}$.
(3)设点C关于$x$轴的对称点为$C'$，则$C'$的坐标为(0，-3)，连接$AC'$交$x$轴于点P，此时$PA + PC$有最小值，最小值为$AC'$的长.
设直线$AC'$的表达式是$y = kx + n$，把$C'(0,-3)$，$A(1,2)$的坐标代入，得$\begin{cases}n=-3\\k + n = 2\end{cases}$，解得$\begin{cases}k = 5\\n=-3\end{cases}$.
∴直线$AC'$的表达式为$y = 5x-3$，当$y = 0$时，$5x-3 = 0$，解得$x=\frac{3}{5}$.
∴点P的坐标是$(\frac{3}{5},0)$.