《2025年综合应用创新题典中点九年级数学下册冀教版》

12. [2024石家庄桥西区期末] 如图，AB是⊙O的直径，点D在直径AB上（D与A，B不重合），CD⊥AB且CD = AB，连接CB，与⊙O交于点F，在CD上取一点E，使EF与⊙O相切.
(1)求证：EF = EC；
(2)若D是OA的中点，AB = 4，请直接写出BF的长.
　　　　　　　　　　　　　

答案：

(1)[证明]如图,连接OF,则OF=OB,
∴∠OFB=∠B.
　
∵EF与⊙O相切于点F,
∴EF⊥OF.
　
∴∠OFE=90°.
∴∠EFC+∠OFB=180°−∠OFE=90°.
　
∵CD⊥AB,
∴∠CDB=90°.
∴∠C+∠B=90°.
　
∵∠OFB=∠B,
∴∠EFC=∠C.
∴EF=EC.
(2)[解]BF的长为$\frac{12}{5}$.　[点拨]如图,连接AF.
　
∵AB是⊙O的直径,∠CDB=90°,
　
∴∠AFB=90°=∠CDB.
　　又
∵∠B=∠B,
∴△AFB∽△CDB.
　
∴$\frac{BF}{BD}=\frac{AB}{CB}$.
　
∵AB=4,
　　　　　　　　　　　　　　　　　
　
∴OA=OB=$\frac{1}{2}$AB=2.
　
∵D是OA的中点，
∴OD=$\frac{1}{2}$OA=1.
　
∴BD=OB+OD=2+1=3.
　　又
∵CD=AB=4,
　
∴CB=$\sqrt{BD^{2}+CD^{2}}=\sqrt{3^{2}+4^{2}} = 5$.
　
∴BF=$\frac{AB\cdot BD}{CB}=\frac{4\times3}{5}=\frac{12}{5}$.

13. 如图，在矩形ABCD中，AD = 8，E是边AB上一点，且AE = 1/4AB. ⊙O经过点E，与边CD所在的直线相切于点G（∠GEB为锐角），与边AB所在直线相交于另一点F，且EG：EF = √5：2. 当边AD或BC所在的直线与⊙O相切时，求AB的长.
　　　　　　　　　　　　　

答案：
[解]连接GO并延长交AB于点M,连接OE.
∵⊙O与CD所在直线相切于点G，
∴OG⊥CD.
　又
∵AB//CD,
∴OG⊥AB.
∴EM=FM=$\frac{1}{2}$EF.
∵EG:EF=$\sqrt{5}$:2,
∴EG:EM=$\sqrt{5}$:1,由勾股定理易得GM:EM=2:1.
　易知GM=AD=8,
∴EM=4.
　设⊙O的半径为R,在Rt△EOM中,OM=8−R,由勾股定理得R²=4²+(8−R)²,解得R=5.
　当边AD所在的直线与⊙O相切时，如图①,易知AM=5,
∵EM=4,
∴AE=1.
　又
∵AE=$\frac{1}{4}$AB,
∴AB=4;
　当边BC所在的直线与⊙O相切时,如图②,
∵EM=4,易知MB=5,
∴EB=9,
∵AE=$\frac{1}{4}$AB,
∴EB=$\frac{3}{4}$AB.
∴AB=12.
　故AB的长是4或12.
　　　　　

14. 如图，⊙O的半径为√3，等边三角形ABC的顶点B的坐标为（2，0），顶点A在⊙O上运动.
(1)当点A在x轴正半轴上时，求点C的坐标.
(2)点A在运动过程中，是否存在直线AB与⊙O相切？若存在，请直接写出点C的坐标.
(3)设点A的横坐标为x，△ABC的面积为S，求S与x之间的函数关系式，并求出S的最大值与最小值.
　　　　　　　　　　　　

答案：

(1)[解]若点A在x轴的正半轴上,则点A的坐标为($\sqrt{3}$,0),
∴等边三角形ABC的边长为2 - $\sqrt{3}$.
　　当点C在x轴上方时,过点C作CD⊥AB于点D.
　　由等边三角形的性质可得CD=$\frac{\sqrt{3}}{2}$AC=$\frac{2\sqrt{3}-3}{2}$，AD=$\frac{1}{2}$AC=$\frac{2 - \sqrt{3}}{2}$.
　　故可得点C的坐标为($\frac{2+\sqrt{3}}{2}$，$\frac{2\sqrt{3}-3}{2}$).
　　当点C在x轴下方时，由对称性可知，点C的坐标为($\frac{2+\sqrt{3}}{2}$，$-\frac{2\sqrt{3}-3}{2}$).
　　综上所述,点C的坐标为($\frac{2+\sqrt{3}}{2}$，$\frac{2\sqrt{3}-3}{2}$)或($\frac{2+\sqrt{3}}{2}$，$-\frac{2\sqrt{3}-3}{2}$).
(2)存在.点C的坐标为($\frac{5}{2}$，$\frac{\sqrt{3}}{2}$)或($\frac{5}{2}$，$-\frac{\sqrt{3}}{2}$)或(1，0).
[点拨]①当点A在x轴上方时，分以下两种情况:
　如图①,当点C在AB右侧时，过点C作CE⊥x轴于点E,连接OA.
　　　　　　　　　　　　　　　　
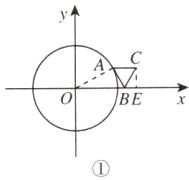
∵直线AB与⊙O相切，
　
∴OA⊥AB.
　
∴∠OAB=90°.
　
∵OB=2,OA=$\sqrt{3}$，
　
∴sin∠OBA=$\frac{\sqrt{3}}{2}$，BC = AB=$\sqrt{2^{2}-(\sqrt{3})^{2}} = 1$.
　
∴∠OBA=60°.
∴∠CBE=60°.
　
∴CE=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$，BE=$\frac{1}{2}$BC=$\frac{1}{2}$.
　
∴OE=OB+BE=$\frac{5}{2}$.
　
∴点C的坐标为($\frac{5}{2}$，$\frac{\sqrt{3}}{2}$).
　　如图②,当点C在AB左侧时，连接OA,同①可知，∠OBA=60°，BC=1.
　　又
∵∠ABC=60°，
　
∴点C在x轴上，
　
∴OC=OB−BC=2−1=1.
　　　　　　　　　　　　　　　　　
　
∴点C的坐标为(1，0).
　　②当点A在x轴下方时，由对称性可知，点C的坐标为($\frac{5}{2}$，$-\frac{\sqrt{3}}{2}$)或(1，0).
　　综上所述,点C的坐标为($\frac{5}{2}$，$\frac{\sqrt{3}}{2}$)或($\frac{5}{2}$，$-\frac{\sqrt{3}}{2}$)或(1，0).
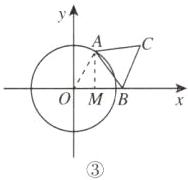
(3)如图③,连接OA,过点A作AM⊥OB于点M,则OM=x.
　
∴在Rt△OAM中,AM²=OA²−OM²=3−x²,
　
∴在Rt△BAM中,AB²=AM²+BM²=(3−x²)+(2−x)²=7−4x,
　
∴易得S=$\frac{\sqrt{3}}{4}$AB²=$\frac{\sqrt{3}}{4}$(7−4x)=-$\sqrt{3}$x+$\frac{7\sqrt{3}}{4}$.
　　由题意得-$\sqrt{3}$≤x≤$\sqrt{3}$.
　
∵-$\sqrt{3}$＜0,
　　　　　　　　　　　　　　　　　
　
∴当x = -$\sqrt{3}$时,S的值最大，最大值为3+$\frac{7\sqrt{3}}{4}$,
　　当x=$\sqrt{3}$时,S的值最小，最小值为-3+$\frac{7\sqrt{3}}{4}$.