第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1. 如图,已知抛物线$y=-x^{2}+bx+c$与$x$轴的一个交点为$A(-1,0)$,对称轴为直线$x = 1$.
(1)求该抛物线的表达式及顶点$C$的坐标;
(2)设对称轴交$x$轴于点$M$,连接$AC$,$CM$,请在$x$轴的正半轴上找一点$D$,使$\triangle ACM$与$\triangle CMD$相似但不全等,求出点$D$的坐标.
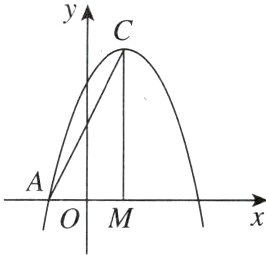
(1)求该抛物线的表达式及顶点$C$的坐标;
(2)设对称轴交$x$轴于点$M$,连接$AC$,$CM$,请在$x$轴的正半轴上找一点$D$,使$\triangle ACM$与$\triangle CMD$相似但不全等,求出点$D$的坐标.

答案:
【解】
(1)由抛物线$y=-x^{2}+bx+c$的对称轴为直线$x = 1$,可得$\frac{b}{2}=1$,解得$b = 2$,
把$A(-1,0)$的坐标代入$y=-x^{2}+2x+c$,得$-1 - 2 + c = 0$,解得$c = 3$,
$\therefore y=-x^{2}+2x+3$.
$\because y=-x^{2}+2x+3=-(x - 1)^{2}+4$,
$\therefore$顶点$C$的坐标为$(1,4)$.
(2)由$x$轴的正半轴上一点$D$,使$\triangle ACM$与$\triangle CMD$相似但不全等,可知点$D$应在$M$右侧,且$MD$和$CM$是对应边,如图.

由题易知$M(1,0)$.设点$D(m,0)$,则$DM = m - 1$.
易知$CM = 4$,$AM = 2$.
$\because\triangle ACM\sim\triangle CDM$,
$\therefore\frac{AM}{CM}=\frac{CM}{DM}$,即$\frac{2}{4}=\frac{4}{m - 1}$,解得$m = 9$.
$\therefore D(9,0)$.
【解】
(1)由抛物线$y=-x^{2}+bx+c$的对称轴为直线$x = 1$,可得$\frac{b}{2}=1$,解得$b = 2$,
把$A(-1,0)$的坐标代入$y=-x^{2}+2x+c$,得$-1 - 2 + c = 0$,解得$c = 3$,
$\therefore y=-x^{2}+2x+3$.
$\because y=-x^{2}+2x+3=-(x - 1)^{2}+4$,
$\therefore$顶点$C$的坐标为$(1,4)$.
(2)由$x$轴的正半轴上一点$D$,使$\triangle ACM$与$\triangle CMD$相似但不全等,可知点$D$应在$M$右侧,且$MD$和$CM$是对应边,如图.

由题易知$M(1,0)$.设点$D(m,0)$,则$DM = m - 1$.
易知$CM = 4$,$AM = 2$.
$\because\triangle ACM\sim\triangle CDM$,
$\therefore\frac{AM}{CM}=\frac{CM}{DM}$,即$\frac{2}{4}=\frac{4}{m - 1}$,解得$m = 9$.
$\therefore D(9,0)$.
2. [2024西安雁塔区校级模拟] 如图,已知抛物线$L:y = ax^{2}-5ax + c(a\neq0)$与$x$轴交于$A(1,0)$与$B$点,与$y$轴交于点$C(0,4)$,抛物线$L'$与$L$关于原点成中心对称,且$A$的对应点为$A'$.
(1)求抛物线$L$的表达式,并直接写出$L'$的表达式;
(2)在$x$轴上方的抛物线$L$上有一点$M$,点$M$在抛物线$L'$上的对应点为$M'$,若四边形$MAM'A'$的面积为20,请求出点$M$的坐标.

(1)求抛物线$L$的表达式,并直接写出$L'$的表达式;
(2)在$x$轴上方的抛物线$L$上有一点$M$,点$M$在抛物线$L'$上的对应点为$M'$,若四边形$MAM'A'$的面积为20,请求出点$M$的坐标.

答案:
【解】
(1)$\because$抛物线$L$与$x$轴交于$A(1,0)$与$B$点,与$y$轴交于点$C(0,4)$,
$\therefore\begin{cases}a - 5a + c = 0,\\c = 4,\end{cases}$解得$\begin{cases}a = 1,\\c = 4.\end{cases}$
$\therefore$抛物线$L$的表达式为$y = x^{2}-5x + 4$.
抛物线$L'$的表达式为$y=-x^{2}-5x - 4$.
(2)$\because A(1,0)$,$\therefore A'(-1,0)$,$\therefore AA' = 2$.
设$M(x,x^{2}-5x + 4)$,则$x^{2}-5x + 4>0$.
易知$S_{四边形AMA'A'}=\frac{1}{2}AA'\cdot2(x^{2}-5x + 4)=20$,
$\therefore x^{2}-5x + 4 = 10$.
$\therefore x = 6$或$x = -1$.
$\therefore M(-1,10)$或$(6,10)$.
(1)$\because$抛物线$L$与$x$轴交于$A(1,0)$与$B$点,与$y$轴交于点$C(0,4)$,
$\therefore\begin{cases}a - 5a + c = 0,\\c = 4,\end{cases}$解得$\begin{cases}a = 1,\\c = 4.\end{cases}$
$\therefore$抛物线$L$的表达式为$y = x^{2}-5x + 4$.
抛物线$L'$的表达式为$y=-x^{2}-5x - 4$.
(2)$\because A(1,0)$,$\therefore A'(-1,0)$,$\therefore AA' = 2$.
设$M(x,x^{2}-5x + 4)$,则$x^{2}-5x + 4>0$.
易知$S_{四边形AMA'A'}=\frac{1}{2}AA'\cdot2(x^{2}-5x + 4)=20$,
$\therefore x^{2}-5x + 4 = 10$.
$\therefore x = 6$或$x = -1$.
$\therefore M(-1,10)$或$(6,10)$.
3. 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”. 已知点$A$,$B$,$C$,$D$分别是“果圆”与坐标轴的交点,抛物线的表达式为$y=\frac{1}{2}x^{2}-2x - 6$,$AB$为半圆的直径,$M$为圆心,则这个“果圆”被$y$轴截得的“弦”$CD$的长为_______.


答案:
$2\sqrt{3}+6$【点拨】如图,连接$MC$.

$\because$抛物线的表达式为$y=\frac{1}{2}x^{2}-2x - 6$,
$\therefore$点$D$的坐标为$(0,-6)$.
$\therefore OD$的长为$6$.
设$y = 0$,则$0=\frac{1}{2}x^{2}-2x - 6$,
解得$x = -2$或$x = 6$.
$\therefore A(-2,0)$,$B(6,0)$.
$\therefore OA = 2$,$OB = 6$,$M(2,0)$,$\therefore AB = 8$,$OM = 2$.
$\therefore MC=\frac{1}{2}AB = 4$.
在$Rt\triangle COM$中,$OC=\sqrt{MC^{2}-OM^{2}}=2\sqrt{3}$,
$\therefore CD = CO + OD = 2\sqrt{3}+6$.
$2\sqrt{3}+6$【点拨】如图,连接$MC$.

$\because$抛物线的表达式为$y=\frac{1}{2}x^{2}-2x - 6$,
$\therefore$点$D$的坐标为$(0,-6)$.
$\therefore OD$的长为$6$.
设$y = 0$,则$0=\frac{1}{2}x^{2}-2x - 6$,
解得$x = -2$或$x = 6$.
$\therefore A(-2,0)$,$B(6,0)$.
$\therefore OA = 2$,$OB = 6$,$M(2,0)$,$\therefore AB = 8$,$OM = 2$.
$\therefore MC=\frac{1}{2}AB = 4$.
在$Rt\triangle COM$中,$OC=\sqrt{MC^{2}-OM^{2}}=2\sqrt{3}$,
$\therefore CD = CO + OD = 2\sqrt{3}+6$.
查看更多完整答案,请扫码查看


