《2025年综合应用创新题典中点九年级数学下册冀教版》

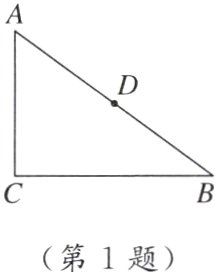
1. 母题教材P3例 如图，△ABC为直角三角形，∠C = 90°，AC = 6，BC = 8，以点C为圆心，CA长为半径作⊙C，则△ABC斜边的中点D与⊙C的位置关系是（ ）
A. 点D在⊙C上 B. 点D在⊙C内
C. 点D在⊙C外 D. 不能确定
　　　　

答案： B

2. 已知一次函数y = kx + 2的图像经过第一、二、四象限，以坐标原点O为圆心，r为半径作⊙O. 若对于符合条件的任意实数k，一次函数y = kx + 2的图像与⊙O总有两个公共点，则r的最小值为_______.

答案： 2

3. 如图，在△ABC中，∠ABC = 90°，∠BAC = 30°，BC = 2，O是边AB上一点，以点O为圆心，OA长为半径在边AB的右侧作半圆O，交边AB于点P，交边AC于点Q. 关于结论Ⅰ，Ⅱ，下列判断正确的是（ ）
结论Ⅰ：当BQ的长度最短时，半圆O的半径为√3；
结论Ⅱ：当BQ = BC时，BQ与半圆O相切，且OP = BP.
A. 只有结论Ⅰ对 B. 只有结论Ⅱ对
C. 结论Ⅰ，Ⅱ都对 D. 结论Ⅰ，Ⅱ都不对
　　　　

答案：
C [点拨]如图①,当BQ⊥AC时,BQ的长度最短.
∵AP是半圆O的直径,
∴∠AQP=90°.
∴PQ⊥AC.
∴点P与点B重合.
∵∠ABC=90°,∠BAC=30°,BC=2,
∴AC=2BC=4.
∴AP = AB=$\sqrt{AC^{2}-BC^{2}}=\sqrt{4^{2}-2^{2}} = 2\sqrt{3}$.
∴OP=$\frac{1}{2}$AP=$\sqrt{3}$.
∴半圆O的半径为$\sqrt{3}$.故结论Ⅰ对.
　　　　　　
　当BQ=BC时,如图②,连接OQ.
∵∠ABC=90°,∠BAC=30°,
∴∠C=60°.
∴△QBC是等边三角形.
∴∠QBC=60°.
∴∠ABQ=∠ABC−∠QBC=30°.
∵OQ=OA,
∴∠OQA=∠BAC=30°.
∴∠BOQ=∠OQA+∠BAC=60°.
∴∠OQB=180°−∠ABQ−∠BOQ=90°,即BQ⊥OQ.
∵OQ是半圆O的半径，
∴BQ与半圆O相切.
　在Rt△BOQ中,∠OBQ=30°,
∴OB=2OQ=2OP.
∴OP=BP,故结论Ⅱ对.

4. 如图，已知AB是⊙O的直径，BD是⊙O的弦，点P是⊙O外一点，PC⊥AB，垂足为点C，PC与BD相交于点E，连接PD，PD = PE，延长PD交BA的延长线于点F.
(1)求证：PD是⊙O的切线；
(2)若DF = 4，PE = 7/2，cos∠PFC = 4/5，请直接写出BE的长.
　　　　　　　　　　　　　　　　　　　　

答案：

(1)[证明]如图，连接OD.
∵OD=OB,
∴∠ODB=∠OBD.
∵PD=PE,
∴∠PDE=∠PED.
∵PC⊥AB,
∴∠BCE=90°.
　　　　　　　　　　　　　　　　
∴∠OBD+∠BEC=90°.
∵∠PED=∠BEC,
∴∠BEC=∠PDE.
∴∠ODB+∠PDE=90°,即∠PDO=90°.
　又
∵OD是⊙O的半径，
∴PD是⊙O的切线.
(2)[解]BE的长为$\sqrt{5}$.
[点拨]
∵PD=PE=$\frac{7}{2}$,
∴PF=PD+FD=$\frac{15}{2}$.
　　在Rt△PFC中,
∵cos∠PFC=$\frac{CF}{FP}=\frac{4}{5}$，
∴CF=6.
　　在Rt△ODF中,
∵cos∠PFC=$\frac{DF}{OF}=\frac{4}{5}$，
∴OF=5.
　
∴OC=CF−OF=1,OD=$\sqrt{OF^{2}-FD^{2}}=\sqrt{5^{2}-4^{2}} = 3$，
　
∴OB=OD=3.
∴BC=OB−OC=2.
　
∵PC=$\sqrt{PF^{2}-CF^{2}}=\frac{9}{2}$，
∴CE=PC−PE=1.
　
∴BE=$\sqrt{BC^{2}+CE^{2}}=\sqrt{2^{2}+1^{2}}=\sqrt{5}$.

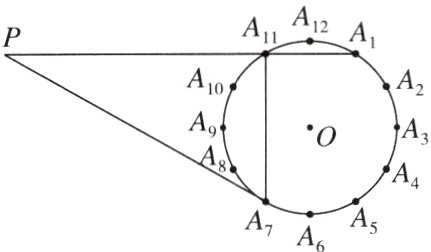
5. 如图，⊙O的半径为6，将该圆周12等分后得到表盘模型，其中整钟点为Aₙ（n为1～12的整数），过点A₇作⊙O的切线交A₁A₁₁的延长线于点P.
(1)通过计算比较直径和劣弧A₇A₁₁哪个更长.
(2)连接A₇A₁₁，则A₇A₁₁和PA₁有什么位置关系？请简要说明理由.
(3)求PA₇的长度.
　　　　　　　　　　　　　　　　　　

答案：

(1)[解]由题意得$\overset{\frown}{A_{7}A_{11}}$对应的圆心角为120°，
∴$\overset{\frown}{A_{7}A_{11}}$的长为$\frac{120\pi\cdot6}{180}=4\pi＞12$.
∴$\overset{\frown}{A_{7}A_{11}}$更长.
(2)PA₁⊥A₇A₁₁.
　　理由:如图,连接A₁A₇.
　　易得A₁A₇是⊙O的直径，
　　　　　　　　　　　　　
　
∴∠A₇A₁₁A₁=90°.
　
∴PA₁⊥A₇A₁₁.
(3)
∵PA₇是⊙O的切线,
∴PA₇⊥A₁A₇.
　
∴∠PA₇A₁=90°.易知∠PA₁A₇=60°,
∵A₁A₇=12,
　
∴PA₇=A₁A₇·tan 60° = 12$\sqrt{3}$.