《2025年综合应用创新题典中点九年级数学下册冀教版》

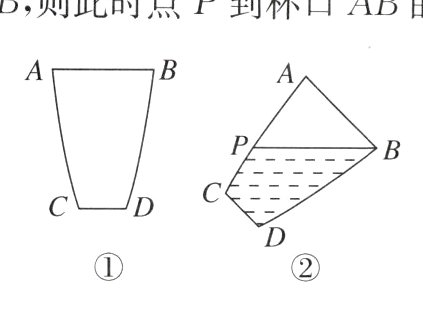
6. [2024宿迁模拟] 一种玻璃水杯的截面如图①所示，其左右轮廓线AC，BD为某一抛物线的一部分，杯口AB = 8 cm，杯底CD = 4 cm，且AB//CD，杯深为12 cm，如图②，若盛有部分水的水杯倾斜45°(即∠ABP = 45°)，水面正好经过点B，则此时点P到杯口AB的距离为 ( )

A. 5 cm
B. 6 cm
C. 5$\sqrt{2}$ cm
D. 7 cm

答案：
D 【点拨】建立如图所示的平面直角坐标系，作$\angle ABP = 45^{\circ}$，$BP$交抛物线于点$P$. 作$PE\perp x$轴于点$E$.

易知$A(-4,0)$，$B(4,0)$，$C(-2,-12)$.
设抛物线的表达式为$y = a(x + 4)(x - 4)$，
将$(-2,-12)$代入，
得$-12 = a(-2 + 4)(-2 - 4)$，
解得$a = 1$，
$\therefore y=(x + 4)(x - 4)=x^{2}-16$.
$\because\angle ABP = 45^{\circ}$，$\angle PEB = 90^{\circ}$，
$\therefore\angle BPE = 45^{\circ}$. $\therefore\angle EPB=\angle EBP$. $\therefore EP = EB$.
设$P(x_{P},y_{P})$. 则$EP = EB = 4 - x_{P}$，
$\therefore y_{P}=x_{P}-4$，$\therefore x_{P}^{2}-16=x_{P}-4$，
解得$x_{P}=4$（舍去）或$x_{P}=-3$，
$\therefore y_{P}=-3 - 4=-7$. $\therefore PE = 7cm$.
$\therefore$题中所求的点$P$到杯口$AB$的距离为$7cm$.

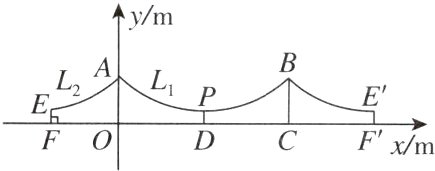
7. [2024陕西] 一条河上横跨着一座宏伟壮观的悬索桥. 桥梁的缆索$L_{1}$与缆索$L_{2}$均呈抛物线型，桥塔AO与桥塔BC均垂直于桥面，如图所示，以O为原点，以直线FF'为x轴，以桥塔AO所在直线为y轴，建立平面直角坐标系.
已知：缆索$L_{1}$所在抛物线与缆索$L_{2}$所在抛物线关于y轴对称，桥塔AO与桥塔BC之间的距离OC = 100 m，AO = BC = 17 m，缆索$L_{1}$的最低点P到FF'的距离PD = 2 m. (桥塔的粗细忽略不计)
(1)求缆索$L_{1}$所在抛物线的函数表达式；
(2)点E在缆索$L_{2}$上，EF⊥FF'，且EF = 2.6 m，FO＜OD，求FO的长.

答案： 【解】
(1)由题意，知$AO = 17m$，$\therefore A(0,17)$.
$\because OA = BC$，$OC = 100m$，缆索$L_{1}$的最低点$P$到$FF'$的距离$PD = 2m$，$\therefore$抛物线的顶点$P$的坐标为$(50,2)$.
故可设缆索$L_{1}$所在抛物线的函数表达式为$y = a(x - 50)^{2}+2$.
将点$A(0,17)$的坐标代入，得$2500a + 2 = 17$. $\therefore a=\frac{3}{500}$.
$\therefore$缆索$L_{1}$所在抛物线的函数表达式为$y=\frac{3}{500}(x - 50)^{2}+2$.
(2)由题意，知缆索$L_{1}$所在抛物线与缆索$L_{2}$所在抛物线关于$y$轴对称，
且由
(1)知缆索$L_{1}$所在抛物线为$y=\frac{3}{500}(x - 50)^{2}+2$，
$\therefore$缆索$L_{2}$所在抛物线为$y=\frac{3}{500}(x + 50)^{2}+2$.
令$y = 2.6$，则$2.6=\frac{3}{500}(x + 50)^{2}+2$.
解得$x=-40$或$x=-60$.
$\therefore FO = 40m$或$FO = 60m$.
又$\because FO\lt OD = 50m$，$\therefore FO$的长为$40m$.

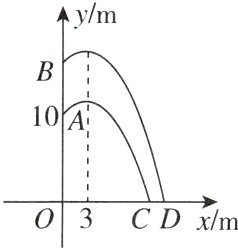
8. 情境题 生活应用 高楼火灾越来越受到重视，某区消防中队开展消防技能比赛，如图，在一废弃高楼距地面10 m的点A和其正上方点B处各设置了一个火源. 消防员来到火源正前方，水枪喷出的水流看作抛物线的一部分(水流出口与地面的距离忽略不计)，第一次灭火时，站在水平地面上的点C处，水流恰好到达点A处，且水流的最大高度为12 m，待A处的火熄灭后，消防员退到点D处，调整水枪进行第二次灭火，使水流恰好到达点B处，已知点D到高楼的水平距离为12 m，假设两次灭火时水流的最高点到高楼的水平距离均为3 m，建立如图所示的平面直角坐标系，水流的高度y(m)与到高楼的水平距离x(m)之间的函数关系式为$y = ax^{2}+bx + c$.
(1)求消防员第一次灭火时水流所在抛物线的表达式；
(2)若两次灭火时水流所在抛物线的形状相同，求A，B之间的距离；
(3)若消防员站在到高楼水平距离为9 m的地方，想要扑灭距地面高度为8～12 m范围内的火苗，当水流最高点到高楼的水平距离始终为3 m时，请直接写出a的取值范围.

答案： 【解】
(1)由题意可知，第一次灭火时水流最高点的坐标为$(3,12)$，
$\therefore$设水流所在抛物线的表达式为$y = a(x - 3)^{2}+12$.
$\because$点$A(0,10)$在抛物线上，
$\therefore10 = a(0 - 3)^{2}+12$，解得$a = -\frac{2}{9}$，
$\therefore y = -\frac{2}{9}(x - 3)^{2}+12$.
答：消防员第一次灭火时水流所在抛物线的表达式为$y = -\frac{2}{9}(x - 3)^{2}+12$.
(2)$\because$两次灭火时水流所在抛物线的形状相同，且水流的最高点到高楼的水平距离均为$3m$，
$\therefore$可设第二次灭火时水流所在抛物线的表达式为$y = -\frac{2}{9}(x - 3)^{2}+m$.
由题意可知该抛物线过点$(12,0)$，
$\therefore0 = -\frac{2}{9}(12 - 3)^{2}+m$，解得$m = 18$.
$\therefore y = -\frac{2}{9}(x - 3)^{2}+18$.
令$x = 0$，则$y = 16$，$\therefore B(0,16)$.
又$\because A(0,10)$，
$\therefore AB = 16 - 10 = 6(m)$.
答：$A$，$B$之间的距离为$6m$.
(3)$-\frac{4}{9}\leqslant a\leqslant-\frac{8}{27}$ 【点拨】由题意可知，灭火过程中$y$与$x$始终满足$y = a(x - 3)^{2}+h$，将$(9,0)$代入后可得$0 = 36a+h$，$\therefore h=-36a$.
$\therefore y = a(x - 3)^{2}-36a$.
当抛物线经过点$(0,12)$时，$12 = a(0 - 3)^{2}-36a$，
解得$a = -\frac{4}{9}$.
当抛物线经过点$(0,8)$时，$8 = a(0 - 3)^{2}-36a$，
解得$a = -\frac{8}{27}$.
$\therefore-\frac{4}{9}\leqslant a\leqslant-\frac{8}{27}$.