《2025年综合应用创新题典中点九年级数学下册冀教版》

8. [母题 教材P15习题B组T1]如图，直线AB，CD相交于点O，∠AOD = 30°，半径为2 cm的⊙P的圆心在直线AB上，且位于点O左侧，距离点O 10 cm处. 如果⊙P以2 cm/s的速度沿直线AB由A向B的方向移动，那么________后⊙P与直线CD相切.

答案： 3s或7s　[点拨]①当圆在直线CD的左侧与其相切时,
设圆心为P1,切点为E.连接P1E,
则P1E⊥CD,
∴∠P1EO = 90°.
∵P1E = 2cm,∠AOD = 30°,
∴P1O = 4cm.
∴PP1 = PO - P1O = 10 - 4 = 6(cm).
∴$\frac{6}{2}=3(s)$;
②当圆在直线CD的右侧与其相切时,设圆心为P2,同理
易得P2O = 4cm,
∴PP2 = PO + P2O = 10 + 4 = 14(cm),
∴$\frac{14}{2}=7(s)$.
综上,3s或7s后⊙P与直线CD相切.

9. [2024石家庄校级模拟]如图，⊙O是△ABC的外接圆，P是BC延长线上一点，连接OA，OC，PA，且∠PCA = ∠PAB，D是AC的中点，OD的延长线交AP于点Q，连接CQ，下列结论：①∠B = ∠AOD；②OQ垂直平分AC；③直线PA和CQ都是⊙O的切线；④CQ//AO. 其中正确的结论是___________.

答案： ①②③　[点拨]
∵D是AC的中点,
∴AD = CD.
∵OA = OC,
∴OQ⊥AC,∠AOD = ∠COD = $\frac{1}{2}$∠AOC.
∴OQ垂直平分AC,
∵∠B = $\frac{1}{2}$∠AOC,
∴∠B = ∠AOD,故①②正确.
∵∠PCA = ∠PAB,
∴∠PAC = 180° - ∠P - ∠PCA = 180° - ∠P - ∠PAB = ∠B.
∵∠B = ∠AOD,
∴∠PAC = ∠AOD.
易知∠ADO = 90°,
∴∠PAO = ∠PAC + ∠OAC = ∠AOD + ∠OAC = 90°.
∴PA⊥OA.
∵OC = OA,
∴∠OCA = ∠OAC.
∵OQ垂直平分AC,
∴QC = QA.
∴∠QCA = ∠QAC.
∴∠QCO = ∠OCA + ∠QCA = ∠OAC + ∠QAC = ∠QAO = 90°.
∴CQ⊥OC.
∵OA,OC都是⊙O的半径,
∴直线PA和CQ都是⊙O的切线,故③正确;
假设CQ//AO成立,则∠AQC = 180° - ∠QAO = 90°,
∴∠AOC = 360° - ∠AQC - ∠QAO - ∠QCO = 90°.
∴∠B = $\frac{1}{2}$∠AOC = 45°.
∴∠B不一定为45°,
∴CQ//AO不一定成立,故④错误.

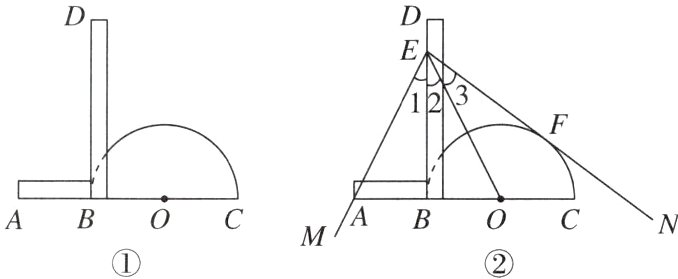
10. 如图①是一种简易三分角器的示意图，其中AB与半圆O的直径BC在同一直线上，且AB的长度与半圆O的半径相等，DB垂直AC于点B，DB足够长. 三分角器的使用方法如图②所示，若要把∠MEN三等分，只需适当放置三分角器，使DB经过∠MEN的顶点E，点A落在边EM上，半圆O与另一边EN恰好相切，切点为F，则EB，EO就把∠MEN三等分了.
（1）请根据题意写出已知和结论；
（2）请证明这一方法的正确性.

答案：
(1)[解]已知:点A,B,O,C在同一直线上,EB⊥AC,
垂足为B,以BC为直径作半圆O,AB = OB,∠MEN的
顶点E在DB上,边EM过点A,边EN与半圆O相切
于点F.
结论:EB,EO是∠MEN的三等分线.
(2)[证明]
∵EB⊥AC,
∴∠ABE = ∠OBE = 90°.
∵AB = OB,BE = BE,
∴△ABE≌△OBE(SAS).
∴∠1 = ∠2.
连接OF,
∵EN切半圆O于点F,
∴OF⊥EN.
又
∵OB = OF,OB⊥EB,
∴∠2 = ∠3.
∴∠1 = ∠2 = ∠3.
∴EB,EO是∠MEN的三等分线.

11. [新视角 新定义型题]定义：P，Q分别为两个图形G1，G2上任意一点，当线段PQ的长度存在最小值时，就称该最小值为图形G1和G2的“近距离”；当线段PQ的长度存在最大值时，就称该最大值为图形G1和G2的“远距离”. 如图，在平面直角坐标系xOy中，点A(-2，3)，B(-2，-4)，C(2，-4)，D(2，3).
（1）线段AB与线段CD的“近距离”为________；
（2）⊙M的圆心在x轴正半轴上，半径为1，若⊙M与CD相切于点E，且点M在点E的左侧，则⊙M与线段AB的“近距离”为________，此时⊙M与四边形ABCD的“远距离”为________.

答案：
(1)4　　
(2)2;6　　[点拨]
(1)
∵点A(-2,3),B(-2,-4),C(2,-4),D(2,3),AD⊥AB,
∴AB//CD,AD = BC = 4.
∴线段AB与线段CD的“近距离”为4.
(2)
∵⊙M与CD相切于点E,圆心在x轴正半轴上,半径为1,
且点M在点E的左侧,
∴易知⊙M与y轴相切.
∴⊙M与线段AB的“近距离”为2.
连接BM,易知BM = $\sqrt{3^{2}+4^{2}} = 5$,
∴⊙M与四边形ABCD的“远距离”为5 + 1 = 6.