《2025年综合应用创新题典中点九年级数学下册冀教版》

5. [2024邯郸期末]如图，抛物线y = (x - 1)² + n与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C(0,-3)，连接AC，点D与点C关于抛物线的对称轴对称.
(1)求抛物线的表达式及点D的坐标；
(2)点P是抛物线对称轴上的一动点，当△PAC的周长最小时，求出点P的坐标.
　　　　　　　　　　　　

答案：
【解】
(1)将C(0,-3)的坐标代入抛物线的表达式,得-3=1+n,解得n=-4.
∴抛物线的表达式为y=(x - 1)²-4.
∴抛物线的对称轴为直线x=1.
∵点D与点C关于抛物线的对称轴对称,
∴点D的坐标为(2,-3).
(2)如图,连接AD交抛物线的对称轴于点P.
∵点C与点D关于直线x=1对称,
∴PC=PD.
∴AP+PC=AP+PD=AD.
∴此时AP+PC有最小值.
又
∵AC为定值,
∴此时△APC的周长最小.
令y=0,则0=(x - 1)²-4,解得x=-1或x=3.
∵点A在点B的左侧,
∴点A的坐标为(-1,0).
设直线AD的表达式为y=kx+b,将点D和点A的坐标代入,得{2k + b = -3, -k + b = 0}, 解得{k = -1, b = -1}.
∴直线AD的表达式为y=-x-1.
将x=1代入y=-x-1,得y=-2.
∴当△PAC的周长最小时,点P的坐标为(1,-2).

题型5 二次函数中的面积最值问题
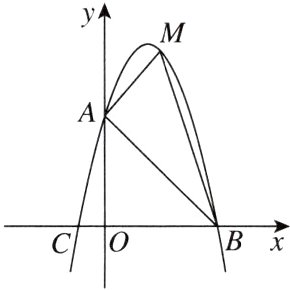
6. 如图，抛物线y = -x² + bx + c与y轴交于点A，与x轴交于点B，C，已知A(0,4)，B(4,0).
(1)求抛物线的表达式，并求出点C的坐标；
(2)点M是抛物线(第一象限内)上的一个动点，连接MA，MB，AB，当△MAB的面积最大时，求点M的坐标；
(3)若点M的坐标固定为(1,6)，Q是抛物线上除M点之外的一个动点，当△ABM与△ABQ的面积相等时，求点Q的坐标.
　　　　　　　　　　　　

答案：
【解】
(1)由题意得{c = 4, -16 + 4b + c = 0}, 解得{b = 3, c = 4}.
则抛物线的表达式为y=-x²+3x+4.
令y=0,则-x²+3x+4=0,解得x=4或x=-1,
故C(-1,0).
(2)如图,过点M作MH//y轴交AB于点H,
由点A,B的坐标得,直线AB的表达式为y=-x+4.
设点M(x,-x²+3x+4),则点H(x,-x+4),
∴MH=-x²+3x+4-(-x+4)=-x²+4x.
则△MAB的面积=1/2MH·OB=1/2×4×(-x²+4x)=-2x²+8x=-2(x - 2)²+8.
∵-2＜0,
∴当x=2时,△MAB的面积最大.
此时点M的坐标为(2,6).
(3)由
(2)知,直线AB的表达式为y=-x+4.
当点Q在直线AB上方时,过点M作直线MR//AB交y轴于点R,由M(1,6)易得直线MR的表达式为y=-x+7,则点R(0,7),则AR=3.
联立y=-x+7和y=-x²+3x+4,得-x+7=-x²+3x+4,解得x=1(舍去)或x=3,即点Q(3,4).
当点Q在直线AB下方时,在y轴上点A下方取点T,使AT=AR,则点T(0,1).
过点T作直线TQ//AB,交抛物线于点Q,
则易知直线TQ的表达式为y=-x+1.
联立y=-x+1和y=-x²+3x+4,得-x+1=-x²+3x+4,解得x=2±√7,
则点Q(2+√7,-1-√7)或(2-√7,-1+√7).
综上,点Q的坐标为(3,4)或(2+√7,-1-√7)或(2-√7,-1+√7).