第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
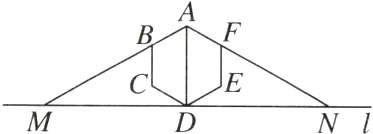
10. [2024邯郸模拟] 如图,过正六边形ABCDEF的顶点D作一条直线l⊥AD于点D,分别延长AB,AF交直线l于点M,N,则∠AMN =________;若正六边形ABCDEF的面积为6,则△AMN的面积为________.

答案:
30°;16 [点拨]如图,连接BE交AD于点O.
∵六边形ABCDEF是正六边形,
∴OA = OB,∠AOB = $\frac{360^{\circ}}{6}=60^{\circ}$.
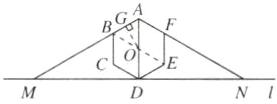
∴△AOB是正三角形,
∴∠OAB = 60°,AB = OA.
过点O作OG⊥AB,则OG = OA·sin 60° = $\frac{\sqrt{3}}{2}$OA.
∵AD⊥MN,
∴∠ADM = 90°.
∴∠AMN = 180° - 60° - 90° = 30°. 同理∠ANM = 30°.
∵正六边形ABCDEF的面积为6,
∴△AOB的面积为1.
∴$\frac{1}{2}$AB·OG = 1.
∴$\frac{\sqrt{3}}{4}$·OA² = 1.
∴OA² = $\frac{4\sqrt{3}}{3}$.
∵∠AMN = ∠ANM = 30°,
∴AM = AN,
又
∵AD⊥MN,
∴DM = DN = $\sqrt{3}$AD = 2$\sqrt{3}$OA,
∴S△AMN = $\frac{1}{2}$MN·AD = $\frac{1}{2}\times2\times2\sqrt{3}$OA×2OA = 4$\sqrt{3}$OA² = 16.
30°;16 [点拨]如图,连接BE交AD于点O.
∵六边形ABCDEF是正六边形,
∴OA = OB,∠AOB = $\frac{360^{\circ}}{6}=60^{\circ}$.

∴△AOB是正三角形,
∴∠OAB = 60°,AB = OA.
过点O作OG⊥AB,则OG = OA·sin 60° = $\frac{\sqrt{3}}{2}$OA.
∵AD⊥MN,
∴∠ADM = 90°.
∴∠AMN = 180° - 60° - 90° = 30°. 同理∠ANM = 30°.
∵正六边形ABCDEF的面积为6,
∴△AOB的面积为1.
∴$\frac{1}{2}$AB·OG = 1.
∴$\frac{\sqrt{3}}{4}$·OA² = 1.
∴OA² = $\frac{4\sqrt{3}}{3}$.
∵∠AMN = ∠ANM = 30°,
∴AM = AN,
又
∵AD⊥MN,
∴DM = DN = $\sqrt{3}$AD = 2$\sqrt{3}$OA,
∴S△AMN = $\frac{1}{2}$MN·AD = $\frac{1}{2}\times2\times2\sqrt{3}$OA×2OA = 4$\sqrt{3}$OA² = 16.
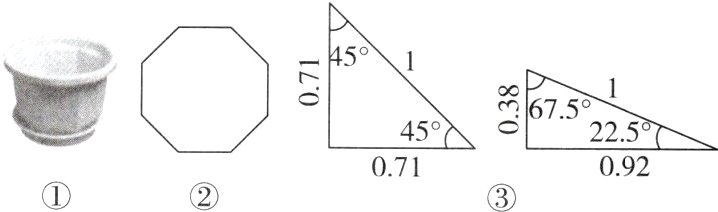
11. (12分) [情境题 生活应用] 如图①,小吴同学在陶艺课中为八角花盆制作圆形托盘,已知八角花盆底部截面是一个正八边形(如图②),请解决下列问题.
(1)求八角花盆底部截面正八边形一个内角的度数.
(2)若八角花盆底部截面正八边形的边长是16 cm,小吴同学制作的圆形托盘半径是22 cm,问:这个托盘是否适用于此八角花盆?(图③中的数据为近似值,供选用)
(1)求八角花盆底部截面正八边形一个内角的度数.
(2)若八角花盆底部截面正八边形的边长是16 cm,小吴同学制作的圆形托盘半径是22 cm,问:这个托盘是否适用于此八角花盆?(图③中的数据为近似值,供选用)

答案:
【解】
(1)
∵正八边形的外角 = $\frac{360^{\circ}}{8}=45^{\circ}$,
∴正八边形的内角 = 180° - 45° = 135°.
(2)如图,设正八边形的中心为点O,连接OA,OB,过点O作OH⊥AB于点H,则∠AOB = $\frac{360^{\circ}}{8}=45^{\circ}$.
∵OA = OB,
∴AH = $\frac{1}{2}$AB = 8 cm,∠AOH = $\frac{1}{2}$∠AOB = 22.5°.
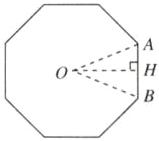
∴sin 22.5° = $\frac{AH}{OA}\approx\frac{0.38}{1}$,
∴OA≈21.1 cm.
∵21.1 cm<22 cm,
∴这个托盘适用于此八角花盆.
【解】
(1)
∵正八边形的外角 = $\frac{360^{\circ}}{8}=45^{\circ}$,
∴正八边形的内角 = 180° - 45° = 135°.
(2)如图,设正八边形的中心为点O,连接OA,OB,过点O作OH⊥AB于点H,则∠AOB = $\frac{360^{\circ}}{8}=45^{\circ}$.
∵OA = OB,
∴AH = $\frac{1}{2}$AB = 8 cm,∠AOH = $\frac{1}{2}$∠AOB = 22.5°.

∴sin 22.5° = $\frac{AH}{OA}\approx\frac{0.38}{1}$,
∴OA≈21.1 cm.
∵21.1 cm<22 cm,
∴这个托盘适用于此八角花盆.
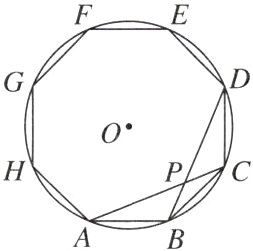
12. (14分)如图,正八边形ABCDEFGH内接于⊙O,连接AC,BD,相交于点P,若⊙O的半径为1.
(1)求AC的长;
(2)求∠APD的度数.
(1)求AC的长;
(2)求∠APD的度数.

答案:
【解】
(1)如图,连接OA,OB,设OB与AC交于点Q,由题意易知QA = QC,OB⊥AC.
∵八边形ABCDEFGH是正八边形,
∴∠AOB = $\frac{360^{\circ}}{8}=45^{\circ}$,
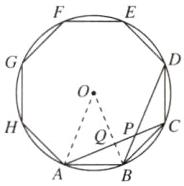
∴QA = OA·sin ∠AOB = 1×sin 45° = $\frac{\sqrt{2}}{2}$,
∴AC = 2QA = $\sqrt{2}$.
(2)由题意可知$\overset{\frown}{AFD}$所对的圆心角为5∠AOB = 225°,
∴∠ABD = $\frac{1}{2}\times225^{\circ}=112.5^{\circ}$.
易知∠BAC = $\frac{1}{2}\times45^{\circ}=22.5^{\circ}$.
∴∠APD = ∠ABD + ∠BAC = 135°.
【解】
(1)如图,连接OA,OB,设OB与AC交于点Q,由题意易知QA = QC,OB⊥AC.
∵八边形ABCDEFGH是正八边形,
∴∠AOB = $\frac{360^{\circ}}{8}=45^{\circ}$,

∴QA = OA·sin ∠AOB = 1×sin 45° = $\frac{\sqrt{2}}{2}$,
∴AC = 2QA = $\sqrt{2}$.
(2)由题意可知$\overset{\frown}{AFD}$所对的圆心角为5∠AOB = 225°,
∴∠ABD = $\frac{1}{2}\times225^{\circ}=112.5^{\circ}$.
易知∠BAC = $\frac{1}{2}\times45^{\circ}=22.5^{\circ}$.
∴∠APD = ∠ABD + ∠BAC = 135°.
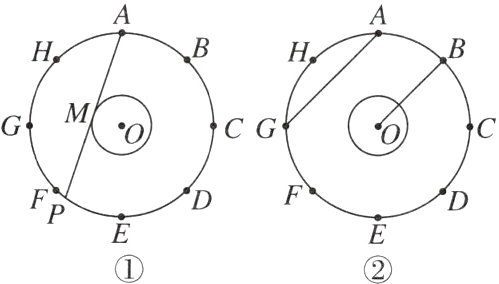
13. (20分)[2024沧州模拟] 如图①和图②,O为两个同心圆的圆心,大圆被八等分,等分点为A,B,C,D,E,F,G,H. 已知两个圆的半径分别为6,2.
(1)如图①,若大圆中的弦AP与小圆相切于点M,求AP的长;
(2)通过计算比较⌢AD的长和小圆的周长的大小;
(3)如图②,连接OB,AG,判断OB和AG的位置关系,并求出点B到直线AG的距离.
(1)如图①,若大圆中的弦AP与小圆相切于点M,求AP的长;
(2)通过计算比较⌢AD的长和小圆的周长的大小;
(3)如图②,连接OB,AG,判断OB和AG的位置关系,并求出点B到直线AG的距离.

答案:
【解】
(1)如图①,连接OA,OM.
∵AP与小圆相切于点M,
∴OM⊥AP.
∴AM = PM.
在Rt△AOM中,OA = 6,OM = 2,
∴AM = $\sqrt{OA^{2}-OM^{2}} = 4\sqrt{2}$,
∴AP = 2AM = 8$\sqrt{2}$.
(2)如图①,连接OD. 由题意得∠AOD = $\frac{360^{\circ}}{8}\times3 = 135^{\circ}$,
∴$\overset{\frown}{AD}$的长为$\frac{135\pi\times6}{180}=\frac{9}{2}\pi$.
∵小圆的周长为2π×2 = 4π,且4π<$\frac{9}{2}\pi$,
∴$\overset{\frown}{AD}$的长大于小圆的周长.
(3)如图②,连接OA,OG.
由题意得∠AOB = $\frac{360^{\circ}}{8}=45^{\circ}$,∠AOG = $\frac{360^{\circ}}{8}\times2 = 90^{\circ}$,OA = OG,
∴∠OAG = ∠OGA = 45°.
∴∠OAG = ∠AOB.
∴OB//AG.
过点O作ON⊥AG于点N,则ON = OA·sin 45° = 3$\sqrt{2}$.
∵OB//AG,
∴点B到直线AG的距离为3$\sqrt{2}$.

【解】
(1)如图①,连接OA,OM.
∵AP与小圆相切于点M,
∴OM⊥AP.
∴AM = PM.
在Rt△AOM中,OA = 6,OM = 2,
∴AM = $\sqrt{OA^{2}-OM^{2}} = 4\sqrt{2}$,
∴AP = 2AM = 8$\sqrt{2}$.
(2)如图①,连接OD. 由题意得∠AOD = $\frac{360^{\circ}}{8}\times3 = 135^{\circ}$,
∴$\overset{\frown}{AD}$的长为$\frac{135\pi\times6}{180}=\frac{9}{2}\pi$.
∵小圆的周长为2π×2 = 4π,且4π<$\frac{9}{2}\pi$,
∴$\overset{\frown}{AD}$的长大于小圆的周长.
(3)如图②,连接OA,OG.
由题意得∠AOB = $\frac{360^{\circ}}{8}=45^{\circ}$,∠AOG = $\frac{360^{\circ}}{8}\times2 = 90^{\circ}$,OA = OG,
∴∠OAG = ∠OGA = 45°.
∴∠OAG = ∠AOB.
∴OB//AG.
过点O作ON⊥AG于点N,则ON = OA·sin 45° = 3$\sqrt{2}$.
∵OB//AG,
∴点B到直线AG的距离为3$\sqrt{2}$.

查看更多完整答案,请扫码查看


