《2025年综合应用创新题典中点九年级数学下册冀教版》

8. 如图，在△ABC中，∠B=70°，⊙O是△ABC的内切圆，M，N是切点，连接OA，OC，交⊙O于E，D两点.点F是⌢MN上的一点，连接DF，EF，则∠EFD的度数是_______.
　

答案： 62.5° 【点拨】
∵⊙O是△ABC的内切圆，
∴AO，CO是△ABC的角平分线.
∴∠OAC = $\frac{1}{2}$∠BAC，∠OCA = $\frac{1}{2}$∠BCA.
∵∠B = 70°，
∴∠BAC + ∠BCA = 180° - ∠B = 110°.
∴∠OAC + ∠OCA = $\frac{1}{2}$(∠BAC + ∠BCA) = 55°.
∴∠AOC = 180° - 55° = 125°.
∴∠EFD = $\frac{1}{2}$∠EOD = 62.5°.

9. [2024成都模拟]如图，在平面直角坐标系xOy中，⊙O的半径为1. A，B为⊙O外两点，AB=1. 给出如下定义:平移线段AB，得到⊙O的弦A'B'(A'，B'分别为点A，B的对应点)，线段AA'长度的最小值称为线段AB到⊙O的“平移距离”.若A(4，3)，记线段AB到⊙O的“平移距离”为d，则d的取值范围为____________.
　　　　

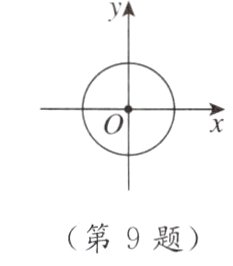
答案： 4≤d≤6

10. (16分)如图，有两块量角器完全重合在一起(量角器的直径AB=4，圆心为O)，保持下面一块不动，上面的一块沿AB所在的直线l向右平移，当圆心与点B重合时，量角器停止平移，此时半圆O与半圆B交于点P，连接AP.
(1)AP与半圆B有怎样的位置关系? 请说明理由.
(2)在量角器半圆O上，点A，B的读数分别为180°，0°时，点P在这块量角器上的读数是多少?
(3)请直接写出图中阴影部分的面积.
　　　　　　　　　　　

答案：
【解】
(1)AP与半圆B相切. 理由如下：
如图，连接PB.
∵AB为半圆O的直径，

∴∠APB = 90°，
∴BP⊥AP.
∵BP为半圆B的半径，
∴AP与半圆B相切.
(2)如图，连接OP，易得△OPB为等边三角形，
∴∠POB = 60°.
∵在量角器半圆O上，点A，B的读数分别为180°，0°，
∴点P在这块量角器上的读数是60°.
(3)图中阴影部分的面积为$\frac{2\pi}{3}+\sqrt{3}$. 【点拨】由
(2)得∠POB = 60°，∠PBO = 60°，
∴∠PBC = 120°.
∵AB = 4，
∴等边三角形POB的边长为2，
∴S阴影 = S扇形PBC - (S扇形POB - S△POB) = $\frac{120·\pi·2^{2}}{360}-(\frac{60·\pi·2^{2}}{360}-\frac{\sqrt{3}}{4}×2^{2})=\frac{4\pi}{3}-\frac{2\pi}{3}+\sqrt{3}=\frac{2\pi}{3}+\sqrt{3}$.

11. (18分)如图①，AB为半圆的直径，点O为圆心，AF为半圆的切线，过半圆上的点C作CD//AB交AF于点D，连接BC.
(1)连接DO，若BC//OD，求证:CD是半圆的切线；
(2)如图②，当线段CD与半圆交于点E时，连接AE，AC，请直接写出∠AED和∠ACD的数量关系.
　　　　　　　　

答案：

(1)【证明】如图①，连接OC.
∵CD//AB，BC//OD，
∴四边形BODC是平行四边形.

∴OB = CD.
∵OA = OB，
∴CD = OA.
∴四边形ADCO是平行四边形.
∵AF为半圆的切线，
∴AB⊥AD.
∴四边形ADCO是矩形.
∴OC⊥CD.
∵OC是半圆的半径，
∴CD是半圆的切线.
(2)【解】∠AED + ∠ACD = 90°. 【点拨】如图②，连接BE.
∵AB//CD，
∴∠AED = ∠BAE.
∵AB为半圆的直径，
∴∠AEB = 90°.

∴∠BAE + ∠ABE = 90°.
∵∠ACD = ∠ABE，
∴∠AED + ∠ACD = 90°.

12. (18分)如图，MN=8，以线段MN上一点O为圆心，OM，ON的长为半径在MN的同侧分别作圆心角相等的扇形MOA，扇形NOB，连接MB，AB，AN.
(1)若AB=MB，则∠MOA=_______；
(2)当∠MOA=135°时，若BM与扇形AOM所在的圆相切于点M，求tan∠ABO的值.
　　　　　　　　

答案：
【解】
(1)120° 【点拨】如图，在△AOB和△MOB中，
$\begin{cases}AB = MB\\OA = OM\\OB = OB\end{cases}$

∴△AOB≌△MOB(SSS).
∴∠1 = ∠2.
∵扇形MOA和扇形NOB的圆心角相等，
∴∠MOA = ∠BON.
∴∠MOA - ∠2 = ∠BON - ∠2，即∠1 = ∠3.
∴∠1 = ∠2 = ∠3 = 60°.
∴∠MOA = ∠1 + ∠2 = 60° + 60° = 120°.
(2)
∵BM与扇形AOM所在的圆相切于点M，
∴∠OMB = 90°.
∵∠AOM = ∠BON，
∴∠AOM - ∠AOB = ∠BON - ∠AOB. 即∠BOM = ∠NOA. 又
∵OM = OA，OB = ON，
∴△BMO≌△NAO.
∴∠OAN = ∠OMB = 90°.
∵∠MOA = 135°，
∴∠BOM = ∠AON = 45°，
∴∠BOA = 90°，
∴tan∠ABO = $\frac{AO}{BO}=\frac{AO}{ON}$. 在Rt△OAN中，cos∠AON = $\frac{OA}{ON}=\cos 45^{\circ}=\frac{\sqrt{2}}{2}$.
∴tan∠ABO = $\frac{\sqrt{2}}{2}$.