《2025年综合应用创新题典中点九年级数学下册冀教版》

1. 如图，正五边形ABCDE内接于⊙O，连接OC，OD，则∠BAE - ∠COD = （ ）
A. 60° B. 54° C. 48° D. 36°
　　　

答案： D

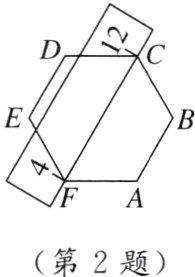
. [2024霸州期末] 将一个特殊的直尺按如图所示的方式放置在正六边形ABCDEF上，顶点C，F分别对应直尺上的刻度12和4，则AB与CF之间的距离为 （ ）
A. 8 B. 2$\sqrt{3}$ C. 4$\sqrt{3}$ D. 4
　　　

答案：
B　[点拨]如图,设正六边形ABCDEF的中心为O,连接OA,过点A作AG⊥CF于点G,由题意可知,CF=12 - 4 = 8,
∵六边形ABCDEF是正六边形，
∴易知△AOF是正三角形.
　　　　　　　　　　　　　　　　　　
∴OF=OC=AF=4.
∴AG = $\frac{\sqrt{3}}{2}$AF = 2$\sqrt{3}$，即AB与CF之间的距离为2$\sqrt{3}$

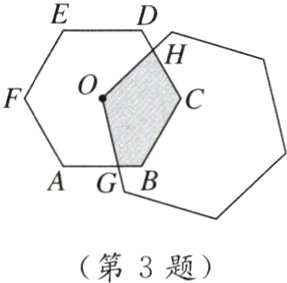
3. [2024张家口模拟] 一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合，且与边AB，CD分别交于点G，H（如图）. 图中阴影部分的面积记为S，三条线段GB，BC，CH的长度之和记为l，在大正六边形绕点O旋转的过程中，下列选项中正确的是 （ ）
A. S变化，l不变 B. S不变，l变化
C. S与l均变化 D. S与l均不变
　　

答案： D

4. 如图，点P1～P8是⊙O的八等分点. 若△P1P3P7，四边形P3P4P6P7的周长分别为a，b，则下列正确的是 （ ）
A. a＜b B. a = b
C. a＞b D. a，b大小无法比较
　　　

答案： A

5. 如图，点O是正八边形A1A2…A8外接圆的圆心，连接A4A6.
（1）∠A8 = ________°；
（2）若⊙O的半径为4 cm，则A4A6 = ________cm.
　　　　　　　　　　　　　　　　

答案：

(1)135　
(2)4$\sqrt{2}$
[点拨]
(1)∠A₅ = $\frac{(8 - 2)×180°}{8}$ = 135°.
(2)如图,连接OA₆，OA₄，
∵∠A₆OA₄ = 360°÷8×2 = 90°，
∴A₄A₆ = $\sqrt{4^{2}+4^{2}}$ = 4$\sqrt{2}$(cm).
　　　　　　　　

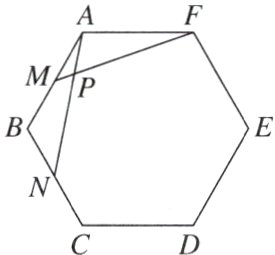
6. 如图，在正六边形ABCDEF中，AM = BN，连接MF，AN交于点P.
（1）求证：△AMF≌△BNA；
（2）求∠FPN的度数.
　　　　　　　　　　　　　　　　

答案：
(1)[证明]
∵六边形ABCDEF是正六边形，
∴AB=AF,∠FAM=∠ABN=120°.
　又
∵AM=BN,
∴△AMF≌△BNA(SAS).
(2)[解]
∵△AMF≌△BNA,
∴∠AFM=∠BAN.
　
∵∠APF=∠AMF+∠BAN=∠AMF+∠AFM=
　　180°−120°=60°,
　
∴∠FPN=180°−∠APF=180°−60°=120°,

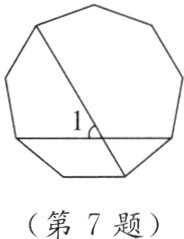
7. 如图，∠1是正九边形两条对角线的夹角，则∠1的度数是 （ ）
A. 45° B. 54° C. 60° D. 72°
　　　　　　　

答案：
C　[点拨]如图,作这个正九边形的外接圆⊙O,连接
BD,OA,OB,OC,OD,
　则∠AOB = $\frac{360°}{9}$ = 40°，∠COD = 2∠AOB = 80°，
∴∠ADB = $\frac{1}{2}$∠AOB = 20°，∠CBD = $\frac{1}{2}$∠COD = 40°.
∴∠1 = ∠ADB + ∠CBD = 20° + 40° = 60°.
　　　　　　　　　　　　　　　　　

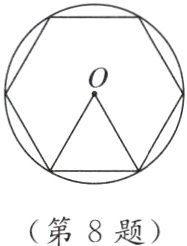
8. 新考向 数学文化 我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”，即利用圆的内接正多边形逼近圆的方法来近似估算，指出“割之弥细，所失弥少. 割之又割，以至于不可割，则与圆周合体，而无所失矣”. “割圆术”孕育了微积分思想，他用这种思想得到了圆周率π的近似值为3.141 6. 如图，⊙O的半径为1，运用“割圆术”，以圆内接正六边形面积近似估计⊙O的面积，可得π的估计值为 $\frac{3\sqrt{3}}{2}$，若用圆内接正十二边形作近似估计，可得π的估计值为 （ ）
A. $\sqrt{3}$ B. 2$\sqrt{2}$ C. 3 D. 2$\sqrt{3}$
　　　

答案：
C　[点拨]如图,设AB是正十二边形的一条边,点O是正十二边形的中心,过点A作AM⊥OB于点M.
　在正十二边形中,∠AOB=360°÷12=30°,
∴AM = $\frac{1}{2}$OA = $\frac{1}{2}$
　　　　　　　　　　　　　　　　　　　　
∴S△AOB = $\frac{1}{2}$OB·AM = $\frac{1}{2}$×1×$\frac{1}{2}$ = $\frac{1}{4}$.
∴正十二边形的面积为12×$\frac{1}{4}$ = 3.
∴3 = 1²×π.
∴π = 3.
∴π的估计值为3.