《2025年综合应用创新题典中点九年级数学下册冀教版》

11. [2024张家口校级月考] 如图，①$y = ax^{2}$，②$y = bx^{2}$，③$y = cx^{2}$，④$y = dx^{2}$，比较$a$，$b$，$c$，$d$的大小，用“＞”连接为___________.

答案：
$a ＞ b ＞ d ＞ c$ 【点拨】如图，因为直线$x = 1$与四条抛物线的交点坐标从上到下依次为$(1,a)$，$(1,b)$，$(1,d)$，$(1,c)$，所以$a ＞ b ＞ d ＞ c$.

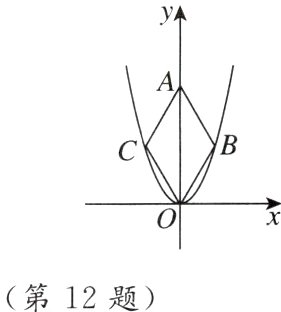
12. 二次函数$y=\sqrt{3}x^{2}$的图像如图，点$O$为坐标原点，点$A$在$y$轴的正半轴上，点$B$，$C$在二次函数$y=\sqrt{3}x^{2}$的图像上，四边形$OBAC$为菱形，且$\angle OBA = 120^{\circ}$，则菱形$OBAC$的面积为_______.

答案：
$2\sqrt{3}$ 【点拨】连接$BC$交$OA$于点$D$，如图所示.
$\because$四边形$OBAC$为菱形，
$\therefore BC\perp OA$，$OA = 2OD$，$BC = 2BD$，$\angle OBD=\frac{1}{2}\angle OBA$.
$\because\angle OBA = 120^{\circ}$，$\therefore\angle OBD = 60^{\circ}$.
$\therefore OD = BD\cdot\tan60^{\circ}=\sqrt{3}BD$.
设$BD = t$，则$OD=\sqrt{3}t$，$\therefore B(t,\sqrt{3}t)$.
把$B(t,\sqrt{3}t)$的坐标代入$y=\sqrt{3}x^{2}$，得
$\sqrt{3}t^{2}=\sqrt{3}t$，解得$t_{1}=0$(舍去)，$t_{2}=1$，
$\therefore BD = 1$，$OD=\sqrt{3}$.
$\therefore BC = 2BD = 2$，$OA = 2OD = 2\sqrt{3}$.
$\therefore$菱形$OBAC$的面积$=\frac{1}{2}\times2\times2\sqrt{3}=2\sqrt{3}$.

13. 如图，平行于$x$轴的直线$AC$分别交函数$y_{1}=x^{2}(x\geqslant0)$与$y_{2}=\frac{x^{2}}{3}(x\geqslant0)$的图像于$B$，$C$两点，过点$C$作$y$轴的平行线交$y_{1}=x^{2}(x\geqslant0)$的图像于点$D$，直线$DE// AC$，交$y_{2}=\frac{x^{2}}{3}(x\geqslant0)$的图像于点$E$，则$\frac{DE}{AB}$的值为________.

答案： $3-\sqrt{3}$ 【点拨】设点$A$的坐标为$(0,k)$.因为$AC// x$轴，点$B$在$AC$上，所以点$B$，$C$的纵坐标与点$A$的纵坐标相同.又因为点$B$在函数$y_{1}=x^{2}(x\geq0)$的图像上，所以点$B$的坐标为$(\sqrt{k},k)$，所以$AB=\sqrt{k}$.因为点$C$在函数$y_{2}=\frac{x^{2}}{3}(x\geq0)$的图像上，所以点$C$的坐标为$(\sqrt{3k},k)$.
因为$CD// y$轴，所以$C$，$D$两点的横坐标相同，即点$D$的横坐标为$\sqrt{3k}$.又因为点$D$在函数$y_{1}=x^{2}(x\geq0)$的图像上，所以点$D$的坐标为$(\sqrt{3k},3k)$.因为$DE// x$轴，所以点$E$的纵坐标与点$D$的纵坐标相同.又因为点$E$在函数$y_{2}=\frac{x^{2}}{3}(x\geq0)$的图像上，所以点$E$的坐标为$(3\sqrt{k},3k)$，
所以$DE = 3\sqrt{k}-\sqrt{3k}$，所以$\frac{DE}{AB}=\frac{3\sqrt{k}-\sqrt{3k}}{\sqrt{k}}=3-\sqrt{3}$.

14. 已知抛物线$y = ax^{2}$与直线$y = 2x - 3$交于点$(1,b)$.
(1)求$a$和$b$的值，并写出抛物线$y = ax^{2}$的表达式.
(2)对于函数$y = ax^{2}$，当$x$取何值时，$y$随$x$的增大而增大？
(3)求该抛物线与直线$y = - 2$的两个交点与该抛物线的顶点所构成的三角形的面积.

答案： 【解】
(1)$\because$点$(1,b)$在直线$y = 2x - 3$上，
$\therefore b = 2\times1 - 3 = - 1$.
$\because$点$(1,b)$，即$(1,-1)$在抛物线$y = ax^{2}$上，
$\therefore - 1 = a\times1^{2}$.$\therefore a = - 1$，
$\therefore$抛物线的表达式为$y = - x^{2}$.
(2)由
(1)知抛物线的表达式为$y = - x^{2}$，$\because - 1 ＜ 0$，
$\therefore$当$x ＜ 0$时，$y$随$x$的增大而增大.
(3)设该抛物线与直线$y = - 2$的两个交点分别为$A$，$B(A$在$B$的左侧)，
当$y = - 2$时，$- 2 = - x^{2}$，$\therefore x=\pm\sqrt{2}$.
$\therefore A$，$B$两点的坐标分别为$(-\sqrt{2},-2)$，$(\sqrt{2},-2)$，
$\therefore AB=\sqrt{2}-(-\sqrt{2})=2\sqrt{2}$.$\because$该抛物线的顶点为$(0,0)$，
$\therefore$所求三角形的面积为$\frac{1}{2}\times2\sqrt{2}\times|-2|=2\sqrt{2}$.

15. 新视角 存在性探究题 如图，抛物线$y = x^{2}$与直线$y = 2x$在第一象限内有一个交点$A$.
(1)求点$A$的坐标.
(2)在$x$轴上是否存在一点$P$，使$\triangle AOP$是以$OP$为底的等腰三角形？若存在，请你求出点$P$的坐标；若不存在，请说明理由.

答案：
【解】
(1)由$\begin{cases}y = x^{2}\\y = 2x\end{cases}$，得$x^{2}=2x$，解得$x_{1}=0$，$x_{2}=2$，因为点$A$在第一象限，所以$x_{A}=2$，所以$y_{A}=4$，所以点$A$的坐标为$(2,4)$.
(2)存在.过点$A(2,4)$作$AB\perp x$轴于点$B$，则$OB = 2$，如图.
当$PB = OB = 2$时，$\triangle AOP$是以$OP$为底的等腰三角形，
此时$OP = 2 + 2 = 4$，所以点$P$的坐标为$(4,0)$.